퀴즈 477 결혼문제3

결혼문제2 를 살짝 꼬아보자.

4쌍이 결혼을 한다. 신랑을 A,B,C, D 라 하고 신부를 X,Y,Z, W 라 하자.

다음과 같은 것이 알려져 있다고 하자.

실제로 누가 누구와 결혼을 하는가?

풀이

확실한 정보만 추려내서 거꾸로 풀면 된다.

A 는 W 랑 커플이 되지 않고
B 도 W 랑 커플이 되지 않고
C 는 Z 랑 커플이 되지 않는다.

마찬가지로

W 는 C 랑
Y 도 C 랑
Z 는 B 랑 커플이 되지 않는다.

이를 표로 나타내면

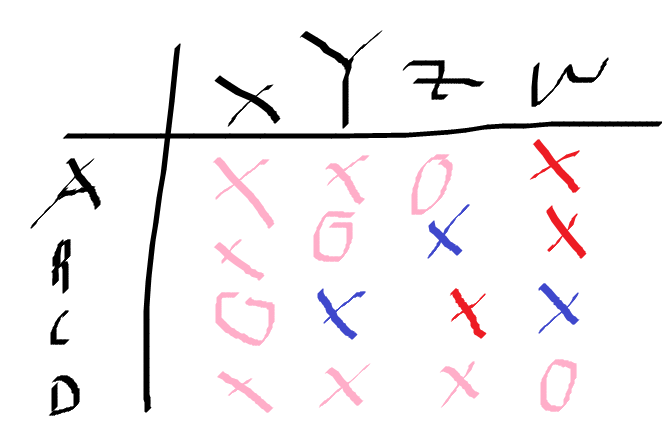
즉

(A,Z), (B,Y), (C,X), (D,W)

1111과 같이 1로만 적히는 수 중에서 2001로 나누어지는 수가 적어도 하나 존재함을 보여라

1, 11, 111, 이를 반복하여 1이 2002개 연속된 수열을 생각해보자.

이 수열의 각 숫자를 2001로 나눌 때 나머지는 0,1, ... , 2000 까지 가능할 것이다. 그런데 전체 숫자는 2002니까 나머지가 같은 두 수가 존재한다. [비둘기집의 원리 이 문제의 핵심 아이디어이다.]

나머지가 같은 두 수를 1이 m 개 다른 수를 1이 n 개 있는 수라 하자. (편의상 m>n) 그러면 두 수의 나머지가 같으니까 두 수를 뺀 수는 2001 로 나누어 떨어질 것이다. 즉

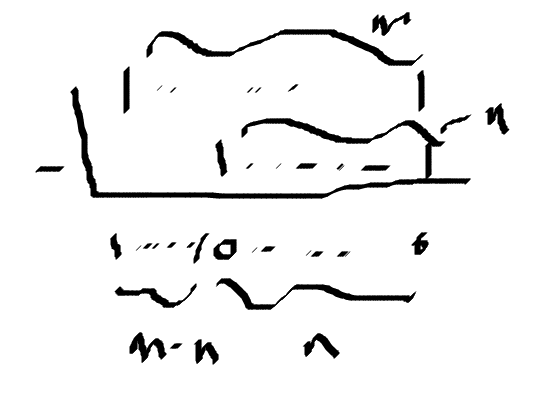
저 수를 좀 더 분석해보자.

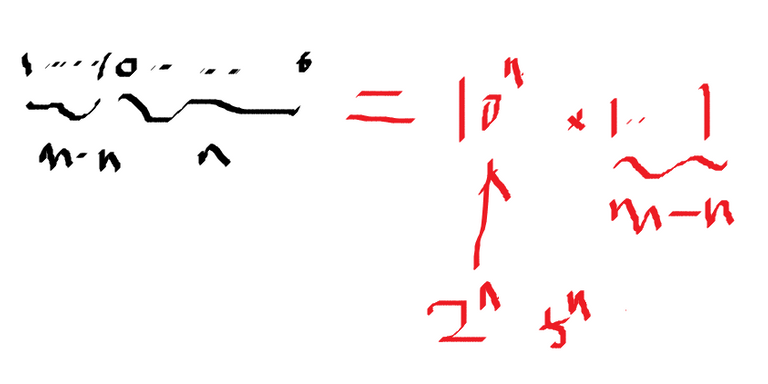
그리고 이 우변은 2001로 나누어 떨어지니까 결국 1...1 (1이 m-n 개 연속된 수) 는 2001로 나누어 떨어지게 되어 1로만 되어 있는 숫자 중에서 2001로 나누어 떨어지는 수는 적어도 한개 존재한다.

나는 마약 단속을 하기 위해 특정 장소를 습격했다.

여기에 5명의 범죄자를 잡았다. 이 중에 경찰에 협조한 자가 있을 것이다. [한명 이상]

시설의 위치와 암호가 매일 바뀌기 때문에

내가 기습 하는 순간, 범죄자들은 누가 협력한 자인지 알게됬다고 한다.

[협력자가 여려명인 경우에도 기습하는 순간 누가 협력자인지 알게 된다고 하자.]

5명의 범죄자를 각각 다른 감옥에 두게 하고 한명씩 불렀다.

A : C 만 범죄자고 나머지는 경찰 편입니다.

B : C와 D 가 범죄자고 저와 A,E 는 모두 경찰편입니다.

C : A 와 B 와 D 는 범죄자이고, 저와 E 는 경찰편입니다.

D : 저를 제외하고 모두 범죄자입니다.

E : 우리는 모두 경찰편입니다.

D가 협력자이다.

가볍게 E 의 말은 거짓이 됨을 알 수 있다. E 가 참이라면 A,B,C,D 모두 같은 말을 해야 한다. [협력자는 협력 순간에 서로를 안다고 했으니 5명 모든 사람이 협력자라면 5명의 말이 일치해야 한다.]

A 가 참이라고 하면, C 만 범죄자이고 A,C,D,E 는 협력자여야 한다. 그런데 A,C,D,E 는 서로 모두 협력자라고 말하지 않는다. 즉 A 는 협력자가 아니다.

비슷한 방법으로 B,C 모두 경찰 편이 아니다.