
빛의 속도가 일정함을 저번 포스팅에서 실험적으로 알아냈음을 소개해드렸습니다.
오늘은 전자기학에서 어떻게 이 빛의 속도가 유도되었는지 알려드리겠습니다.
시작하기에 앞서 수식이 조금 많이 등장할 수 있다는 점 미리 말씀드립니다!!안녕하세요 @chosungyun입니다.
사실, 처음에는 전자기학은 빛과 다르다고 사람들은 생각했었습니다.
전자기학에서 다루는 것은 파동이었고 빛은 입자냐 파동이냐는 논의가 있었으니깐요.
하지만, 전자기파는 곧 빛이고 빛은 곧 전자기파입니다.
그렇기에 전자기학에서 유도한 전자기파의 속도는 곧 빛의 속도임을 의미했습니다.
따라서 지금부터 전자기학에서 어떻게 전자기파의 속도를 구했는지 같이 알아보겠습니다.
우선, 파동방정식을 구해야 합니다.
파동방정식이라는 것은 파동함수가 만족하는 방정식입니다.
파동함수는 어떠한 공간에서 시간과 파의 높이로 설명이 되는 파동을 말합니다.
이러한 파동함수는 운동을 하게 된다면 물리법칙을 만족해야 하며 이를 만족하는 방정식이 파동방정식입니다.
그럼 어떠한 파동함수가 있을 때 이 파동함수가 일정한 속도로 움직인다고 합시다.
일정한 속도로 움직인다면 t만큼의 시간이 흘렀을 때의 파와 t만큼 시간의 전의 파는 vt만큼의 이동거리를 빼주면 정확히 일치하는 동일한 파입니다.
식으로 나타낸다면 다음과 같이 나타낼 수 있습니다.
f(z,t)=g(z-vt,0)
위 식에서 알 수 있듯이 파동함수는 위치 값인 z와 시간 값인 t로 서술됩니다.
파동함수는 다음의 과정에 따라 파동방정식이 유도됩니다.
우선, z-vt를 u라는 임의의 값으로 두고 다음과 같이 z와 t에 대해서 각각 편미분 합니다.

그리고 한 번 더 미분을 해주면 다음과 같은 관계를 가짐을 알 수 있습니다.
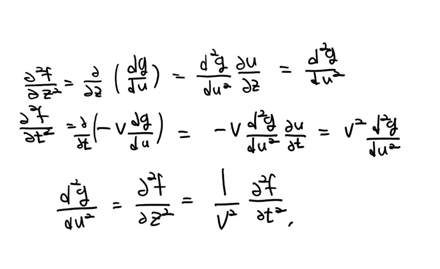
여기서 나오는 이 관계가 파동방정식이며 양자역학과 전자기학에서 두루 쓰이는 중요한 식입니다.
더불어서 만약, 어떤 파동 함수가 있을 때 여기에 작용하는 net force를 기준으로 본다면 다음과 같이 파동방정식을 구할 수 있습니다.

처음 나타나는 그래프는 파동의 어떤 평형점을 기준으로 z가 변함에 따라 나타나는 알짜힘의 변화를 보여줍니다.
일부 부분을 보았을 때 그 부분에서 반대 부분으로 작용하는 장력이 존재할 것이고 세타가 매우 작으니까 sin과 tan값이 비슷해집니다.
그런데 tan값은 그 부위에서의 기울기이고 두 부위에서의 기울기 값을 빼는 변화량은 기울기의 변화량이니깐 f의 z에 대한 이계 도함수로 나타낼 수 있습니다.
또한 여기서 작용한 F는 뉴턴의 제 2법칙에 의해 F=ma로 나타낼 수 있습니다.
여기서 질량은 μ와 ∆z의 곱으로 나타내는데 μ값은 단위길이당 질량으로 ∆z를 곱하게 되면 전체 질량임을 알 수 있습니다.
또한 가속도 a는 파동함수를 시간에 대해 두번 미분한 값이므로 식의 값처럼 구하게 됩니다.
이러한 관계를 확인하면서 앞서 유도한 파동방정식이 파동식과 잘 맞아들어감을 알 수 있습니다.
그럼, 이번에는 전자기파를 기준으로 구해봅시다.

전자기학에서 가장 중요한 식이라 할 수 있는 맥스웰 방정식 4개가 있습니다. 해당 식은 진공이며 공간에 전하가 없을때의 맥스웰 방정식입니다.
모두 각각에 대해서 하나씩 가지는 의미가 많고 중요하기 때문에 설명할 이야기들이 많은 관계로 자세한 설명은 생략하고 각각의 기호가 가지는 뜻은 다음과 같습니다.
∇∙A는 divergence라고 하며 발산하는 정도를 말합니다. 즉, 위 식에서 이 발산하는게 0이라고 했으니 전기장과 자기장이 발산하는 값이 없다는 뜻입니다.
당연히 공간에 전하가 없으니 나아가는 전기장과 자기장은 없다는 것을 직감할 수 있습니다.
물론, 자기장은 원래 발산하지 않습니다.
한편, ∇×A는 curl이라하며 벡터의 회전하는 정도를 말합니다. 이 컬이라는 것의 결과는 각각에 수직한 전기장 혹은 자기장값의 변화량으로 구해집니다.
참고로, ∇×E의 관계가 페러데이 법칙, ∇×B의 관계가 암페어 법칙입니다.
어쨌든, 각각에 대해 위 그림에서와 같이 구하면 파동방정식꼴의 결과를 구할 수 있습니다.
그럼, 오른쪽항의 μ0, ε0는 속도와 관계되는 값임을 예상할 수 있습니다.

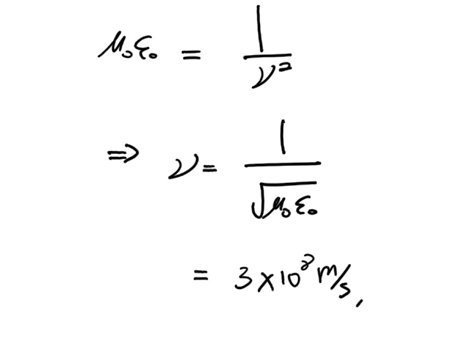
각각의 값들은 위의 상수값이므로 전지기파의 속도는 다음과 같이 30만km/s임을 알 수 있습니다.
이로서, 실험적으로 구한 빛의 속도와 이론적으로 구한 전지기파(빛)의 속도가 일치함을 확인하였습니다.
저번 포스팅과 이번 포스팅까지해서 빛의 속도와 불변성을 알아 보았습니다.
다음 포스팅에서는 갈릴레이 변환을 수정하는 과정에 대해 살펴 보겠습니다.
오늘은 여기서 마칩니다. 감사합니다!!
“해당 포스팅에 사용한 이미지의 출처는 구글이미지입니다”


식은 직접 손으로 쓰신거예요?
넵..ㅎㅎ 수식편집기가 안먹히니 펜으로쓰는게 훨씬 편하네요.
글씨가 악필이라 보기는 안좋지만..ㅠㅠ
진짜 뭐라도 설명하려면 그레디언트, 다이버전스, 컬을 써야되는데, 이걸 쓰는 순간 글은 더이상 대중성을 잃어버린다는 사실이 안타깝습니다ㅎㅎㅎ
vector calculus 수업 가나요! ㅋㅋㅋ
그렇죠..ㅎ 꼭 설명하기위해 필요한 개념들인데 들어가면 어려워지니.. 어쩔수없나봅니다..ㅎㅎ
@beoped님께서 수업해주시면 꼭 보러가야겠습니다.ㅎㅎㅎ
요즘 교과서가 워낙 좋더라고요ㅋㅋ
님께 수업 받는 느낌!
이런분야는 어렵습니다.
과찬이십니다...ㅎㅎ
물리학을 직관적으로 보았을때 어느정도 이해하더라도 이것을 수학을 이용해 이론적으로 기술하고자 한다면 어려워지게되는것 같습니다...
어렵네요 ㅎㅎㅎㅎ
결론은 빛이 전지가파고 둘의 속도가 같다는 건가요?
팔로우 보팅하고갑니다
그렇죠 빛은 전자기파입니다.!!
속도도 30만km/s로 같습니다.
팔로우&보팅 감사합니다. 저도 맞팔할께요~ㅎㅎ
워.....대단하시네요 ㅋ.ㅋ
계산도 어떻게 하는지 모르겠지만 =_=
수식도 아리송...ㅋㅋ;;
그래도 열심히 읽어보고 갑늬다 !!
'빛은 전자기파와 속도가 같다' 결론만 쓰윽...ㅋ.ㅋ
결론이 가장 중요하죠!!ㅎㅎ 감사합니다!
식의 인자는 정확히 다 이해를 못했지만 오랫만에 보내요 미분!
이런식으로 증명해나가는 풀이가 재밌는 것 같아요.
식은 좀 더 머리속에서 컴파일을 시켜야 할 듯 하네요.
재미있게 봐주셔서 감사합니다!ㅎㅎ
천천히 따라가보면 어려운 식은 아니랍니다!
저 맥스웰을 보믄
공간에 간섭물체가 있으면 식이 바뀌니 속도가 달라질 것 같아요
아, 전 전자장을 “이런 젠자장”으로 알고있는
전자기학포기자입니다 ㅋ
잘 보셨습니다ㅎㅎ 그때는 진공에서의 속도보다 작아지게 됩니다!
포기하신것 맞나요?ㅎㅎ 잘 보시는데..^^
빛이 전자기파에 포함된다고 해야할까요 반대라고 해야할까요?
음.. 전자기파중에서 가시광선영역의 파장을 가지면 빛이라고 하니 포한된다고 봐야겠죠..? 둘다 광자로 매개되니..ㅎㅎ
!!! 힘찬 하루 보내요!
어마어마합니다!! 상금이 2억원!!!!!! https://steemit.com/kr/@mmcartoon-kr/5r5d5c
좋은 하루 보내세요~^^
우선 고등학교 수II부터 시작해 주심이 어떠하신지 여쭙습니다. 이거 쉽게 설명해주시면 보팅을 많이 받는다고 장담할 수는 당연히 없습니다만.. ㅠ
빛이 전지가파라니!! 처음 발견한 분들은 '유레카'를 외쳤을 듯 싶습니다. 게다가 세련된 수학으로 증명할 수 있으니 금상첨화였겠습니다.
고등학교 수학부터 하기에는 너무 많은것 같습니다ㅠㅠ
저도 수학을 잘하는 편이 아니기두 하구요...ㅎㅎ
그렇죠! 처음에는 같은 것으로 생각도 못했을테니깐요^^