안녕하세요. @hkkim1030입니다.
[오기 전에 알아두자] 태풍 '노루' 경로 분석하기에서,
'제트류', '해수면 온도 경도', '몬순 기압골'에 대한 포스팅을 요청 받았습니다.
@hunhani님으로부터 태풍 경로에 영향을 미치는 인자인
이것을 설명하기위해,
[아는 것이 힘이다-지구과학#4] 수학으로 바람 이해하기 part1,
[아는 것이 힘이다-지구과학#5] 수학으로 바람 이해하기 part2,
[수학으로 바람 이해하기 part3] 유체를 지배하는 방정식을 알아보자
를 통해 몇 가지 기본적인 지식을 쌓아 보았습니다.
이번 포스팅에서는 위에서 배운 기초지식을 활용하여,
'바람'을 이해하기 위한 '방정식'을 설명해 보고자 합니다.
대기는 기본적으로 유체입니다.
따라서, 유체에 적용되는 방정식을 사용하여 대기 현상을 표현합니다.
유체에 적용되는 방정식은
크게 3가지 입니다.
하나. 연속 방정식 (continuity equation)
둘. 운동량 방정식 (momentum equation)
셋. 열역학 방정식 (thermodynamic equation)
이번 포스팅에서는
운동량 방정식에 대한 설명을 해보고자 합니다.
대기과학에서 운동량방정식은
기압경도력 (pressure gradient force), 중력 (gravitation), 마찰력 (friction), 전향력 (coriolis force)의 결합으로 표현됩니다.
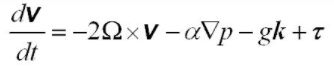
여기에서,
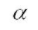 는 specific volume (밀도의 역수)
는 specific volume (밀도의 역수)
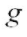 는 grevity
는 grevity
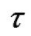 는 friction
는 friction
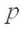 는 기압을 의미합니다.
는 기압을 의미합니다.
보통은 이 방정식을 x (i), y (j), z (k) 방향으로 나누어서 사용을 하기때문에,
저번 포스팅에서 배운 total differentiation 을 적용하고, 중간과정을 생략하면
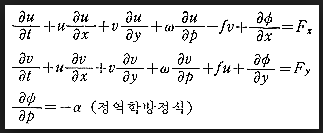
(IMAGE from 기상청 기상백과)
와 같이 간단한 형태로 정리할 수 있습니다.
방정식의 형태를 보면, x축과 y축의 운동량 방정식은 상당히 비슷한 형태를 보이고 있지만,
z축의 운동량 방정식은 간단하게 표현이 됩니다.
z축의 운동량 방정식이 간단하게 표현되는 이유는,
중력과 기압변화가 다른 힘들에 비해 매우 크기 때문입니다.
요즘은 너무 출장이 잦아서 글쓰기가 쉽지 않네요.
중간과정이 생략됐지만, 넓은 양해 부탁드립니다.
그럼 20000.
Cheer Up!
ㅠㅠ 수식과 대기 관련 글들을 보면서 활력(?) 을 얻었는데 ㅠㅠ 요즘 글이 너무 안보여서 혹시 어디 아프신가 했는데 출장 가신거였군요 ㅎㅎ
기회가 되면 한번 중간과정 유도를 해 주세요 ㅎㅎ
그러게요!
그나저나 마크다운은 수식쓰기에 너무 불편합니다ㅠㅠ
http://math.typeit.org/ 를 한번 이용해 보시죠 ㅎㅎ
아니 이렇 훌륭한툴이 있다니!
감사함니당 ㅎ
저도 출장이 잦고 바쁘면 포스팅하는데 많이 제약을 받긴 하더라구요 ㅎㅎ
태풍이 올라올때가 되니 너무 부르는곳이 많네요 ㅠㅠ