퀴즈 279 사각형 안의 점
사각형 안에 N 개의 점이 찍혀 있다. 이것으로 삼각형을 만들려고 하는데(내부의 점과 사각형의 꼭지점을 이용해서), 삼각형의 갯수는?
문제를 풀어보는데 주어진 답에 맞추려면 조건이 더 필요하다. 내부의 점들과 꼭지점으로 생기는 선분이 겹치는 경우를 금하자.
예를 들어
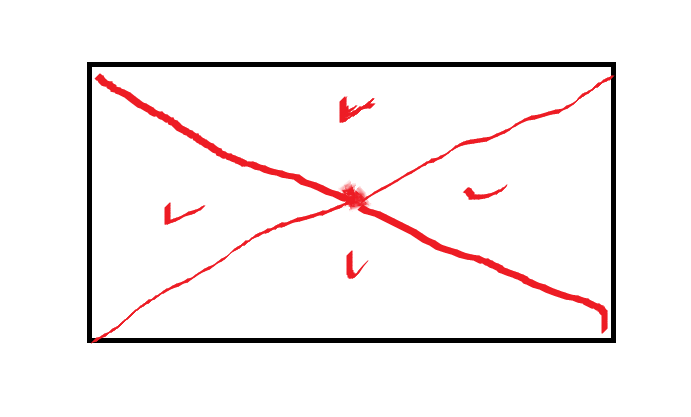
점이 두개 일 때
는 문제에서 요구하는 그림이 아니다. [intersection 이 없어야 한다. ]
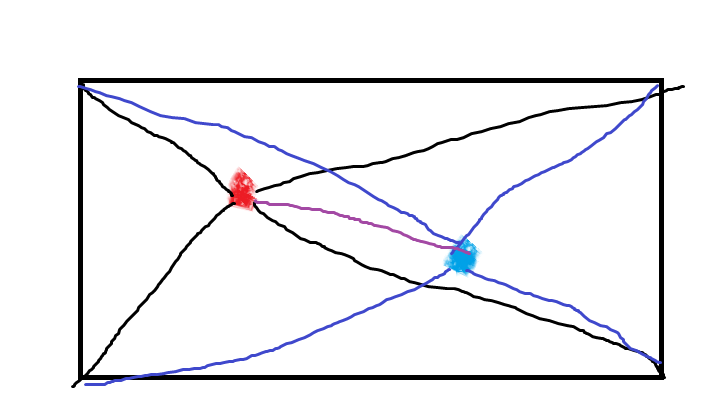
이 문제에서 요구하는 상황은 아래 그림과 같다.
c.f 사각형 내에 점이 4개 찍혀있는 경우에는 10개의 점이 가능하다.
자 쉽게 생각해보자
내부에 점 1개가 찍혀 있을 경우
점이 2개 찍혀 있을 때는
자 여기서 눈치 빠른 사람은 이 문제의 일반화를 바로 찾았을 수도 있다.
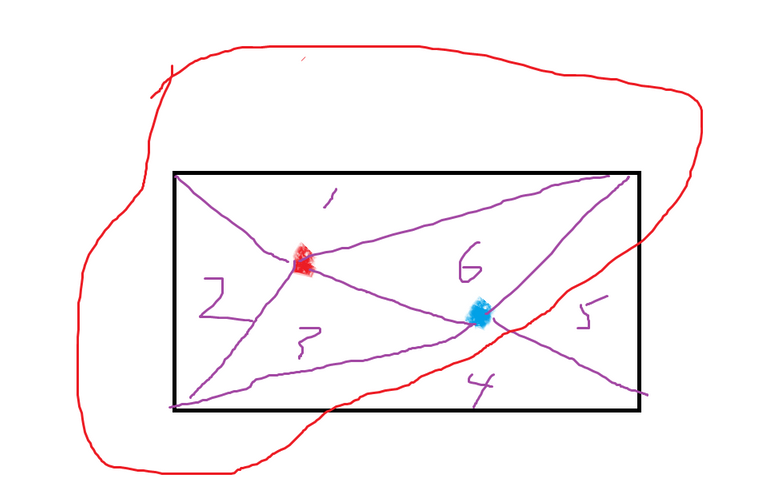
저 그림을 좀 더 살펴보자
빨간 동그라미를 친 부분과 그 외 부분으로 나누어 보자.
음?
그림 안에 이전 그림이 숨어져 있잖아?
이것은?
여기서 이 항의 일반항이 공차가 2이고 초항이 4인 등차수열을 생각해 냈다면
굿!!
a_n = 4+(n-1)2 = 2n+2
[엄밀하게 하려면 수학적 귀납법을 통해 보여야 하지만, 뭐 ㅋㅋㅋ 이것도 쉽다. ]
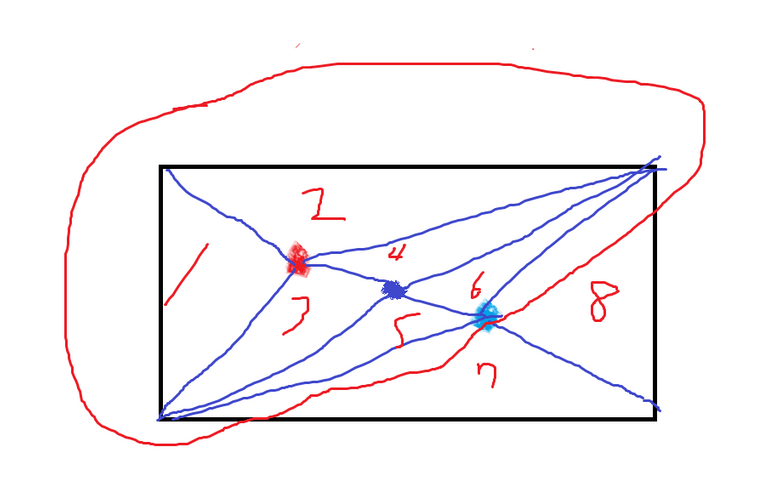
재미 삼아 n=3 일 때를 한번 그려보자 .
물론 교과서에 나와있는 일반적인 풀이는 이런 방식이 아니다.
조금 따분한 방식의 풀이이다.
한번 그 방식대로 문제를 풀어보자면, 삼각형을 만들려면 3점에 180도가 필요하다.
사각형 안에 N 개의 점이 있는 경우 점 하나는 360도를 가지게 된다.
이 말이 무슨 말이냐면,
내부의 점은 하늘색 동그라미 처럼 어떤 방향으로든 뻗어나갈 수 있어서 360도를 만들 수 있다는 것이다.
꼭지점은 물론 90도를 가지고 있고.
즉 360N + 90x4 = 360(N+1) 개의 각도를 가지고 있다.
이를 180으로 나눈 것이 생성할 수 있는 내부의 삼각형 갯수이다.
이로서 앞에서 구한 2N+2 같은 답을 얻는다.
개인적으로 교과서 풀이는 머랄까 마음에 와닿지가 않는다. 처음에 이 풀이를 읽고 뭔 말인지 이해가 잘 안됬다. 또 교과서에는 교차점이 없다 등의 조건이 적혀 있지 않았다. [교차점이 있으면 매우 복잡해진다. 일반적으로 3 점이 삼각형이 되지 않는 경우는 세 점이 모두 일직선에 존재할 때이다. 교차점이 존재하고 임의로 점을 흩뿌리면, 확률 문제가 되어 버린다....]
퀴즈 280 두 개의 알약
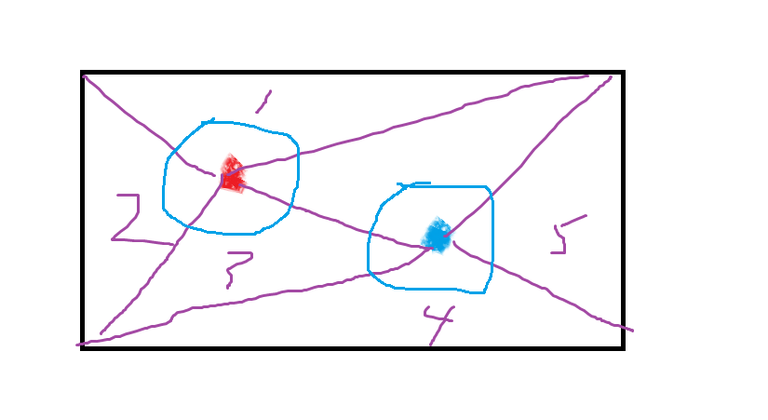
두 개의 명약, A, B 가 있다. 이 A,B 약의 크기와 맛 향이 모두 똑같다. 하나씩 먹으면 치명적인 독이지만 두 약을 같이 복용하면 명약이다. A 약과 B 약은 한개씩 같이 먹어야 하는데, 실수로 A 에서 1개, B 에서 2개를 꺼내고 섞어 버렸다. 이 난처한 상황을 어떻게 돌파해야 하나?
약을 제대로 복용하기 위한 방법을 찾아라
어제 저녁에 푼 문제처럼, 고정관념에서 벗어나자!!!// Feat 퀴즈 277, 278 풀이//플랫랜드!!! 이 문제도 조금 색다른 방법이 필요하다.
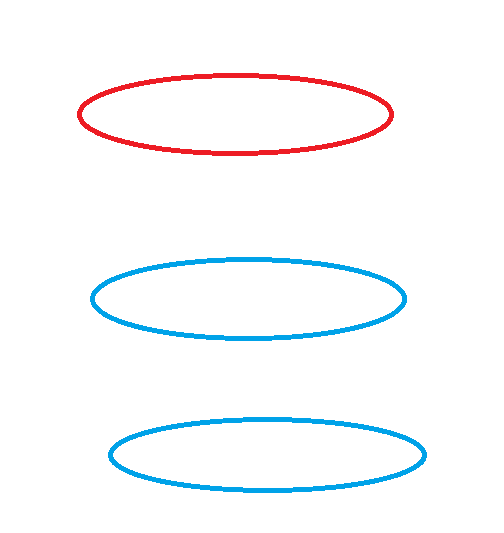
말로 설명하기 힘들어서 또 그림판을 이용해보았다. 편의상 빨간색을 A 파란색을 B 라 하자. 실제로는 구분이 되지 않는다. 여기서는 양만 고려할 것이기에 그냥 구분해 보았다. [ 크게 중요하지 않다. ]
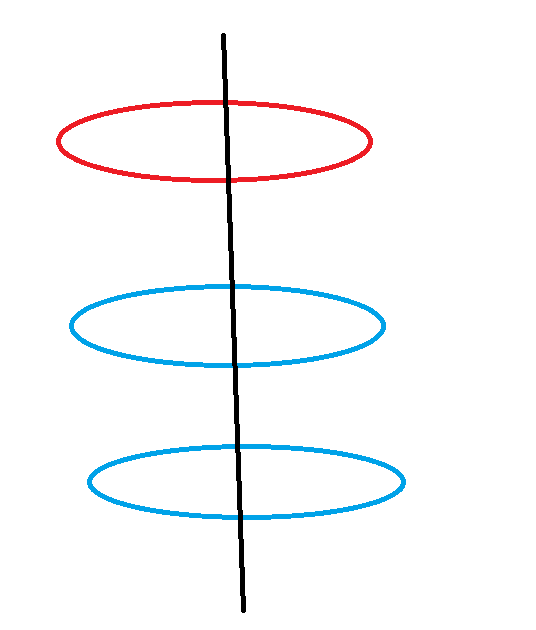
그리고 절단!
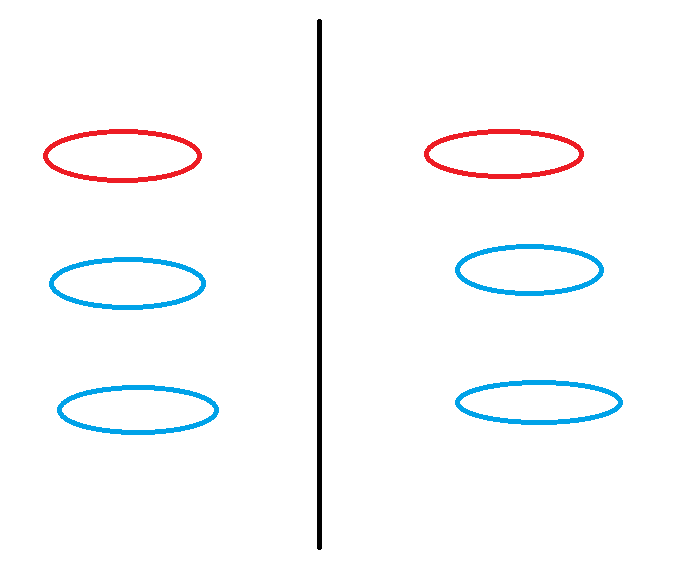
자 이제 집단을 나눈다.
그러면 양쪽 모두 1/2 A 와 B 를 가지게 된다.
A 약통에서 A 를 하나 꺼내 절반으로 자르고 각 집단에 분배하면
왼쪽 오른쪽 모두 1/2 A, 1/2 B 알약 2개가 되어 A 알약, B 알약 1개와 같은 양이 된다!
자름의 미학!
ㅎㅎ
퀴즈글에 그래도 조금이라도 관심을 가지는 사람이 늘어서 기쁘다 ㅎㅎㅎ
예전부터 열심히 참여해주신
@eokkae님, @feelsogood님, @bree1042님 , @dj-on-steem님, @sleeprince님, @seo70님, @glory7님
그리고 @fur2002ks 님 [ㅎㅎㅎ 센스 있는 댓글을 항상 달아주신다 ㅋㅋㅋ]
[이 분들은 좀 어려운 문제들에 댓글을 달아주신다. ]
최근에 참여하시기 시작하신 님들
@naha님, @matsogeum님 @doidoi-sound님, @kiwifi 님
들의 댓글이 있어서 더 기운이 나고 있다!
한번 댓글들 수집해서 이벤트를 열어 볼까? ㅋㅋㅋㅋㅋ
예전 댓글들, 통계 분석하는 스팀잇 툴이 있나 찾아봐야겠다.
심심해서 구글링을 해보니까 누가 내 퀴즈 풀이 글을 인용해 놓았다.
(링크)[https://www.etoland.co.kr/plugin/mobile/board.php?bo_table=etohumor01&wr_id=343505&cpage=1]
오
오오!
굿
@feelsogood 님 아이디가 생각난다 ㅋㅋㅋ 진짜 이 분 아이디 제목 잘 지으신듯!
흠 혹시 feelsolucky 도 있으려나? 오 없네 ㅋㅋㅋ
아이디 선점해 놓아야 하나? ㅋㅋㅋㅋㅋ
I'm feeling so good!
ㅋㅋㅋㅋ
오늘 조합론이랑 외국 퍼즐 책들 사가지고 왔는데 ㅋㅋㅋ
지난번에 사둔 퍼즐 책, 도쿄대생, 등등의 일본 시리즈 책들에서도
좋은 문제 정리하고 응용하고 일반화를 또 해봐야겠다.
책에 없는 풀이를 생각해 낼 때 그 쾌감이란 ㅎㅎ
방금 어머니한테 곧 집에 도착한다고 전화가 왔는데 ㅋㅋㅋ
내 방에 책 사놓고 또 책상에 산더미 같이 쌓아둔걸 보면
주말에 데이트는 안가고 책만보고 컴퓨터 앞에서 드라마만 본다고 또 한소리 하시겠다.
이런 ㅋㅋㅋㅋ
인용될 정도로 잘 풀이를 잘 써주셨네요 bb
퀴즈 많이 진행하셔서 앞으로 더 많이 쓰일거 같아요.
제 아이디 잘 지었다는 칭찬이 있었네요 ^^
Posted using Partiko Android
아... 이해됐어요. 제 답도 틀린건 아니네요.ㅋㅋ
Hi @beoped!
Your post was upvoted by @steem-ua, new Steem dApp, using UserAuthority for algorithmic post curation!
Your UA account score is currently 3.195 which ranks you at #8437 across all Steem accounts.
Your rank has dropped 13 places in the last three days (old rank 8424).
In our last Algorithmic Curation Round, consisting of 181 contributions, your post is ranked at #143.
Evaluation of your UA score:
Feel free to join our @steem-ua Discord server