제어공학분야에서 복소수 평면상에서 유도되는 폴(pole)을 특성을 분석하듯이 머신 러닝에서 선형hypothesis를 끌어내는 과정을 알아보도록 하자. 선형 hypothesis는 별도의 유도 과정 없이 직관적으로 도입하여 사용할 수 도 있겠지만 폴이 2개 이상일 경우의 비선형 문제를 다루기 위한 방법론으로서 미리 다루어 보기로 한다.
전역함수(entire function) f(z)이란 무한대 까지를 포함하는 복소수 평면 전체 즉 z = x+iy 어디에서나 analytic 한 즉 복소수 변수 z에 관해서 미분 가능한 함수를 뜻한다. 또는 z = x+iy 이므로 x 또는 y에 관해서 편미분이 가능하다는 의미이다. 반면에 유리형 함수(meromorphic function)는 이 함수의 특이점(singularities)들이 폴(pole)인 함수를 의미한다.
물리 또는 수학적 공간에서의 공간 좌표들을 독립변수로 하는 함수의 특이점이란 그 점 가까이 접근하게 되면 함수 값이 연속적이긴 하지만 급격히 변화하며 그 점 자체에서는 불연속적으로 무한대 값을 가지게 되어 미분이 불가능하게 되는 특성을 보여준다.
원래의 전역함수가 zero를 가진다면 즉 함수가 0.0 이 되는 z 값이 있다면 그 함수의 역은 폴(pole)을 가지는 셈이다. 머신 러닝에서는 뉴럴 네트워크 관점에서 unique 한 웨이트와 바이아스 값을 사용하여 유도할 수 있는 폴이 존재 하느냐 아니면 과연 몇 세트의 폴 값들이 존재하는지의 문제로 귀착될 수 있다. 그와 같이 폴들이 존재한다면 폴들을 사용하여 유도된 cost 함수에 대해서 경사 하강법을 적용하여 폴들의 값을 결정할 수 있을 것이다.
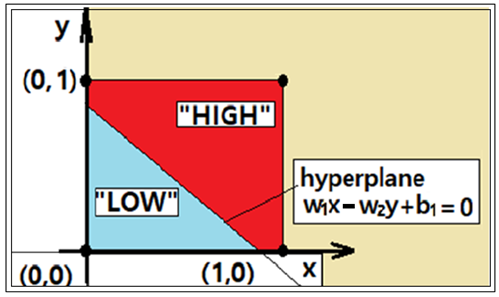
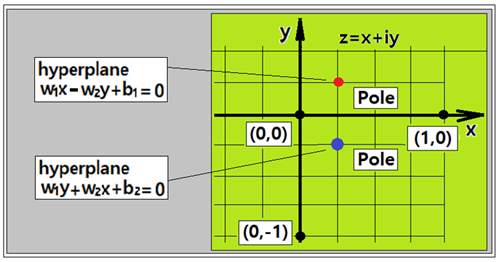
복소수 평면상에서 AND 논리 문제의 특정 점들에서 특정한 order(차수)의 zeros 와 pole을 가지는 전역함수와 유리형 함수를 구성해 보자. 복소수 평면에서 AND 조건은 4개의 점들로 표시되며 (0,0),(1,0),(0,i) 의 3개 점 데이타에 대한 class는 “0” 또는 “LOW” 로 부여되며 (1,i) 점 데이터는 class 가 “1” 또는 “HIGH” 로 부여하면 2가지의 class를 분리 식별하기 위한 hyperplane 설정이 가능해진다.
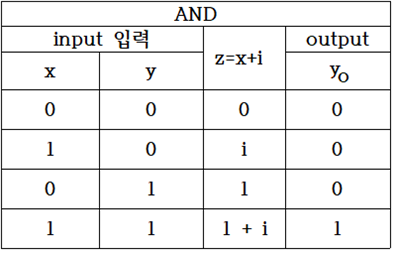
hypothesis 함수가 0.0 의 값을 가지게 되는 즉 zeros에 해당하는 복소수 평면상에서의 폴을 사용하여 hypothesis 함수를 유도하기 위한 복소수 함수를 f(z) 로 두자.
복소수함수 f(z)를 적분하여 h(z) 로 두자.
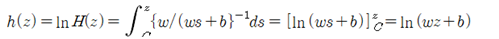
적분 하한 C 는 복소수 함수 H(z)=wz+b 가 실수 값 1.0 이 되는 복소수 평면상에서의 특정한 직선을 나타낸다. 이 식으로부터 복소수 함수 H(z)는 머신 러닝을 위한 복소수 형태의 hypothesis 가 될 수 있음을 알 수 있다.
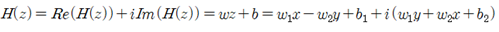
복소수 함수 H(z)와 공액복소수를 사용하여 실수형태의 hypothesis를 구성해 보자.
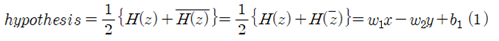
실수 형으로 얻어지는 hypothesis 함수에 출력 데이터를 사용하면서 최소제곱법을 적용하여 웨이트 및 바이아스 값들이 경사하강법에 의해 결정되어야 한다.
또 다른 대안으로서 hypothesis는 다음과 같이 복소수 함수 H(z)의 허수부를 이용하여 구성할 수도 있다.
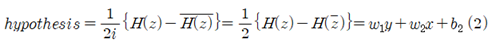
위 두 가지의 hypothesis를 비교해 보면 2개의 웨이트와 1개의 바이아스를 결정하는 문제이므로 어느 것을 사용해도 된다. hypothesis 가 설정되었으면 input 데이터를 사용하여 hypothesis 값과 출력에 해당하는 yo 와의 차이 값을 모두 합산 후 평균한 값인 cost 함수는 머신러닝 과정에서 항상 최소화(minimization)의 대상이 된다.
learning rate = 0.1, 학습 횟수 1000회 일 때에 AND 논리 머신 러닝 계산 결과를 다음과 같이 표로 요약해 보자. 아래의 계산 결과는 소숫이하 5자리에서 반올림하였다.
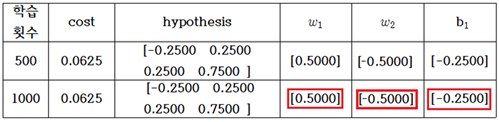
이 계산 결과로부터 AND 논리 머신 러닝 문제의 폴(Pole)을 구해보자. (1)식의 hypothesis를 사용하였으므로 바이아스의 허수 성분은 b2=0.0으로 두고 다음과 같이 폴 값을 계산하자.
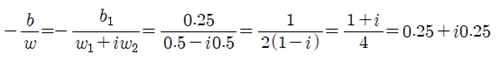
다음 그림에서 1/4 분면에 작도한 폴을 볼 수 있다.
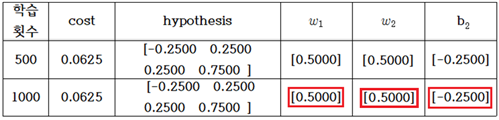
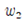의 부호가 바뀌었으며 다음과 같이 폴을 계산할 수 있다. 이때 바이아스의 허수 성분은 b1=0.0 으로 둔다. 아래의 계산 결과는 소숫이하 5자리에서 반올림하였다.
폴의 위치는 위 그림을 참조하자.
Simple Pole 가정에 따라 유도된 hypothesis를 사용하여 학습한 결과 선형의 분리선(classification line, hyperplane)이 결정되었다. 특히 (1) hypothesis 계산 결과와 (2) hypothesis 계산 결과를 비교해 보면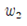 
값의 부호가 바뀌었지만 (2) hypothesis 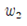의 부호가 (1) hypothesis 와 반대이므로 결국 두 계산 결과는 동일한 것이 된다. 따라서 폴의 위치는 x 축에 대칭으로 서로 다르지만 어느 hypothesis를 사용해도 동일한 hyperplane이 얻어진다.
#multi_variable_lin_reg_AND_pole_01.py
import tensorflow as tf
tf.set_random_seed(777) # for reproducibility
x1_data = [0., 1., 0., 1.]
x2_data = [0., 0., 1., 1.]
y_data = [0., 0., 0., 1.]
#placeholders for a tensor that will be always fed.
x1 = tf.placeholder(tf.float32)
x2 = tf.placeholder(tf.float32)
Y = tf.placeholder(tf.float32)
w1 = tf.Variable(tf.random_normal([1]), name='weight1')
w2 = tf.Variable(tf.random_normal([1]), name='weight2')
b1 = tf.Variable(tf.random_normal([1]), name='bias1')
b2 = tf.Variable(tf.random_normal([1]), name='bias2')
#hypothesis = x1 * w1 - x2 * w2 + b1
hypothesis = x2 * w1 + x1 * w2 + b2
#cost/loss function
cost = tf.reduce_mean(tf.square(hypothesis - Y) )
#cost = tf.reduce_mean(tf.square(hypothesis - Y) )
#Minimize. Need a very small learning rate for this data set
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1)
train = optimizer.minimize(cost)
#Launch the graph in a session.
sess = tf.Session()
#Initializes global variables in the graph.
sess.run(tf.global_variables_initializer())
for step in range(1001):
cost_val, hy_val,w1_val, w2_val, b2_val, _ = sess.run([cost, hypothesis, w1, w2, b1, train],
feed_dict={x1: x1_data, x2: x2_data, Y: y_data})
if step % 500 == 0:
print(step, cost_val, hy_val, w1_val, w2_val, b1_val)
What is this formula?
Posted using Partiko Android
This presents how to derive a linear hypothesis used in machine learning. However, there has not been studied using the method of complex variable. I invented such mathematical method.