지금까지의 머신 러닝 분야 자료를 찾아보면 머신 러닝 이해에 도움을 줄만한 자료가 거의 없는 편이다. 워낙 이 분야 연구 인력이 없었던 탓인 듯하다. 머신 러닝의 수식이래 봤자 선형회귀법에 출발하므로 다음 3차원 그래프에서 볼 수 있겠지만 간단한 3차원 평면 정도이다. 좀 더 나아가 Sigmoid 함수나 Softmax 기법을 사용하게 되면 엑스포넨셜 형 함수에 선형함수를 지수로 가지는 정도이다. 실제 계산 값을 가지고 아래와 같이 한번 그려보면 머신 러닝의 AND 와 OR 로직을 이해하는데 도움이 될 것이다. 아래의 그래프는 라즈베리 파이 B 모델에 공짜로 설치되어 있는 매쓰매티카의 Plot3D 명령을 사용하였다.
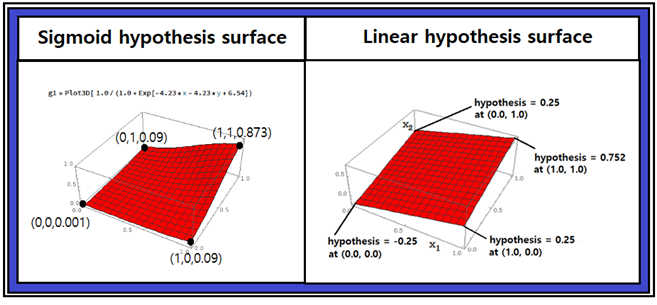
최소제곱법에 의한 AND 로직 머신 러닝에서 얻어진 웨이트와 바이아스를 사용하여 선형 hypothesis의 모양을 그래픽 처리하면 위 오른쪽과 같은 3차원 평면 surface가 얻어진다. Threshold 면 0.5를 적용하면 (0,0), (1,0), (0,1) 점은 Threshold 면 아래에 위치하게 되고 (1,1) 은 Threshold 면 위에 위치하게 된다. 하지만 실제 계산되는 hypothesis 값은 정확한 위치 기준 수직으로 ∓0.25 만큼이 오차를 보여 주는데 논리 상 “LOW” 나 “HIGH” 로 판정함에 문제는 없다.
하지만 Sigmoid 함수를 사용할 경우 hypothesis 계산 값을 모니터링 해 보면 선형 hypothesis 에 비해 훨씬 정확한 값을 준다. 특히 Sigmoid 함수는 엑스포넨셜 항을 포함하고 있어 선형 hypothesis 에 비해 훨씬 복잡한 형태의 곡면을 보여주리라 예상된다.
따라서 Sigmoid 함수를 사용하여 AND 로직 머신 러닝 결과 얻어지는 웨이트와 바이아스 값을 사용하여 hypothesis 곡면을 3차원 그래픽 처리해 보기로 하자.
다음은 Sigmoid hypotheis를 사용하는 AND 로직 머신 러닝 코드 전반부 구조이다.
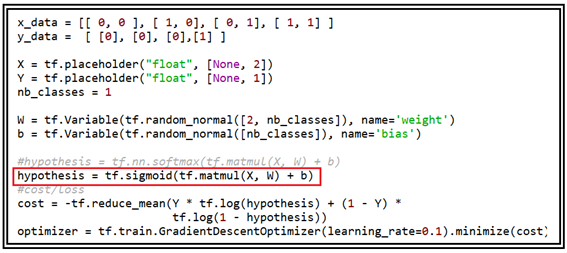
이 코드 내용 중에 hypothesis 계산 내용은 구체적으로 다음과 같이 주어진다.
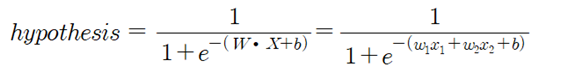
learning rate = 0.1 로 두고 반복학습 횟수를 2000회로 하여 얻어진 계산 결과는 다음 표와 같다.
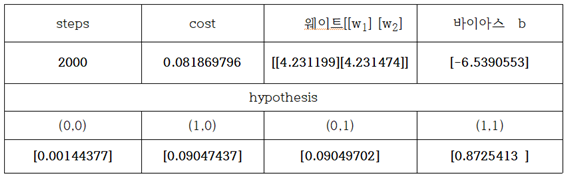
얻어진 웨이트 값 4.23, 4.23 과 바이아스 값 –6.54 를 사용하여 매스매티카로 3차원 그래픽 처리 하도록 하자. 매끈한 형태의 Sigmoid hypothesis 곡면이 얻어졌다. (0,0), (1,0), (0,1) 에서 hypothesis 값이 거의 0에 가까운 반면에 (1,1)에서는 0.873으로 1.0 에 대단히 가까운 곡면을 보여 준다.
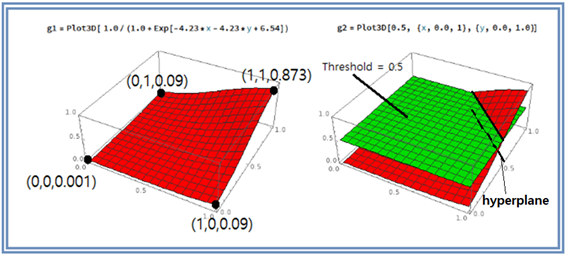
Threshold 면과 Sigmoid hypotheis 와의 교차곡선을 바닥 평면에 투영하면 hyperplane 이 얻어진다.
그 다음 머신 러닝의 제대로 된 이해를 위해서 Sigmoid 보자 좀 더 복잡한 형상으로 예상되는 Softmax 명령에 의한 hypothesis 3차원 곡면 그래픽스로 넘어 가기로 한다.
첨부된 파이선 코드를 실행해 보자. 단 session = tf.Session() 이하 영역에서 indentation 이 무너진 부분을 반드시 복구하여 실행하기 바란다
from matplotlib import pyplot as plt
import numpy as np#sigmoid_AND_logic_01.py
#Sigmoid AND Logic Classifier
import tensorflow as tf
tf.set_random_seed(777) # for reproducibility
x_data = [[ 0, 0 ], [ 1, 0], [ 0, 1], [ 1, 1] ]
y_data = [ [0], [0], [0],[1] ]
X = tf.placeholder("float", [None, 2])
Y = tf.placeholder("float", [None, 1])
nb_classes = 1
W = tf.Variable(tf.random_normal([2, nb_classes]), name='weight')
b = tf.Variable(tf.random_normal([nb_classes]), name='bias')
hypothesis = tf.sigmoid(tf.matmul(X, W) + b)
cost = -tf.reduce_mean(Y * tf.log(hypothesis) + (1 - Y) *
tf.log(1 - hypothesis))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())#hypothesis = tf.nn.softmax(tf.matmul(X, W) + b)
#cost/loss
#Launch graph
for step in range(2001):
sess.run(optimizer, feed_dict={X: x_data, Y: y_data})
if step % 2000 == 0:
print(step, sess.run(cost, feed_dict={X: x_data, Y: y_data}), sess.run(W),sess.run(b))
all = sess.run(hypothesis, feed_dict={
X: [[ 0.0, 0.0 ],[ 1.0, 0.0], [ 0.0, 1.0 ], [ 1.0, 1.0 ]]})
print(all)