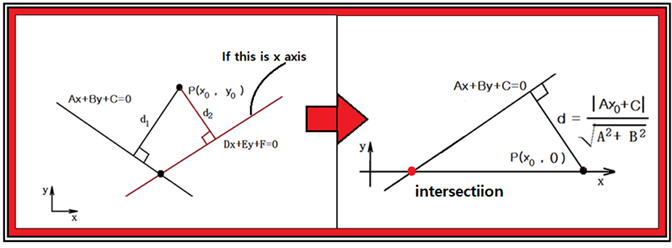
1차 함수와 x 축과의 만나는 점을 찾아내는 문제는 2개의 1차 방정식의 교점을 구하는 문제의 특수한 경우라고 볼 수 있다. 즉 2개의 1차 방정식 중 1개가 x 축이 되는 경우이다. 즉 교점의 좌표를 (x0, y0)라고 한다면 x축과의 교점은 (x0, 0) 이 된다. 따라서 간단한 기하학적 아이디어를 사용하여 least square 기법을 적용해 보기로 한다.
(x,y) 평면에서 1차 방정식 Ax+By+C=0 과 x축 상의 1점 P(x0, 0) 와 최단 직선거리는 그림의 d 로 표현된다. 따라서 y = 0 일 때 방정식의 해는 (x,y) 평면상에서 x축과 교차하는 직선의 교점을 찾는 문제로서 간단히 방정식 Ax + C = 0을 푸는 문제로 바뀐다,
기하학적인 방법으로서 x축에서 방정식 Ax+By+C=0에 수직한 최소 직선거리 d 의 제곱을 cost 함수로 선택하여 그 값을 최소화 하도록 하자.
머신 러닝을 시작하기 위한 초기 조건은 y=0 인 x축 상에 위치한 1점 P (x0, 0) 의 값을 TensorFlow 의 난수 명령을 사용하여 임의의 값 즉 W에서 시작하기로 한다. 여기에서 웨이트 W는 미지의 교점 즉 x 좌표를 뜻한다고 보면 된다.
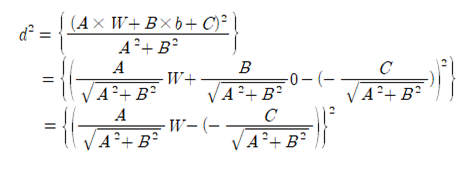
d의 제곱이 위와 같이 표현되면 TensorFlow 모듈을 사용하는 linear regression 예제 코드를 쉽게 변경하여 사용할 수 있음을 알 수 있다. 이 예제에서는 특별히 바이어스 b = 0 인 경우이다.
linear regression 예제 코드에서 hypothesis 와 cost 는 다음과 같이 코딩되었음에 착안하자.
hypothesis = x_train * W + b
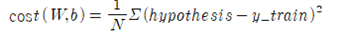
여기서 x_train 과 y_train 은 각각 리스트 데이터 구조를 가진다. 이 코딩을 참조하여 다음과 같이 코드 형태를 수정하자.
hypothesis = A_train * W

여기서 학습 데이터인 A_train, B_train, C_train 은 다음과 같이 리스트 데이터 구조로 주어진다.
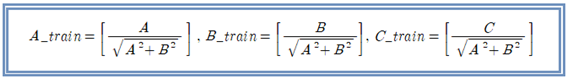
A=1, B=1, C=-1 인 수치 예제를 고려하자. 이 문제는 다음과 같이 2개의 직선의 방정식을 의미한다. 연립하여 풀면 해는 (1, 0)이 된다.
x + y – 1 = 0,
y = 0
1/√2 = 0.707 로 두면 리스트 데이터는 다음 같이 A_train = [ 0.707 ], B_train = [ 0.707 ], C_train = [ 0.707] 으로 설정된다.
learning rate= 0.01에 1000회 학습횟수를 주어 계산된 결과로서 W = 1.0 즉 해는 x = 1.0 임을 알 수 있다.

이 예제에서도 hypothesis 구성이 linear regression 과 다르다는 점에 유의한다. 특히 앞으로 다루게 될 중학교 또는 고등학교 수준의 방정식 문제와 더 나아가 대학 수준의 수치해석 문제들에 있어서도 머신 러닝에 의해서 문제를 해결하려면 문제에 적합한 hypothesis 구성이 전제 되어야 한다.
linear_reg_1wn1chaeqn_01
http://blog.daum.net/ejleep1/543
신기한 방법론이네요! 문제를 어떻게 프레이밍하느냐에 따라 방법론이 갈린다는게 신기하네요ㅎㅎ
머신 러닝 다루는 사람들이 현실적인 어려운 문제들만 학습시키고 있는데 아무리 머신이라해도 사람이 배우는 내용 중에서 특히 중고등학교 기초수학을 제대로 학습을 시켜야 더 많은 분야에서 머신 러닝을 활용할 수 있겠지요