러신 러닝 문제를 코딩한다는 면에서 PyTorch라고 해서 NumPy 나 TensorFlow 와 별다른 특징을 지적할 수는 없을 것이다. 머신 러닝의 목적이 같으므로 결국은 동일하거나 비슷한 결과를 주리라 예상된다. 하지만 훨씬 최근에 출현한 PyTorch는 자체 웹사이트의 예제에 의하면 과학기술 분야의 컴퓨팅 영역에서 오랫동안 파이선 코딩을 뒷받침해 왔던 NumPy 머신 러닝 코드가 GPU 버전으로 업그레이드 가 불가능함을 지적하고 있다. 즉 알고리듬 상으로는 동일하더라도 GPU에 의한 가속 계산 지원이 아쉽게도 안 된다는 점이다. 물론 컴퓨터 언어의 깊숙한 기술적인 내막까지 일반 사용자가 이해하기는 어렵겠지만 적어도 동일한 알고리듬의 머신 러닝 코드를 대상으로 직접 구글 Colabo에 의해 벤치마킹을 해보면 쉽게 이해되리라 본다.

2개의 은닉층으로 구성되는 뉴럴네트워크를 고려하되 PyTorch 나 TensorFlow를 사용하지 않고 일반적으로 과학기술 수치계산을 지원해 주는 NumPy 라이브러리 범위 내에서 코드를 작성해 보자.

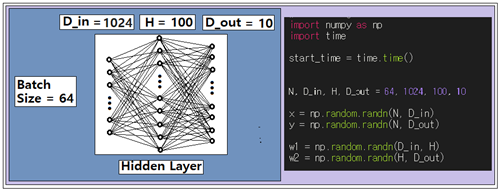
이 문제는 MNIST 수기문자 판독 문제처럼 기술해 보면 다음과 같다. batch job 의 크기가 64이므로 무작위로 64개를 샘플한다. 각 샘플별로 32X32 인 픽셀 구조를 일차원 어레이 형태로 reshape 하여 1000개로 변환한다. 첫 번째 은닉층의 웨이트 매트릭스 W1릏 1024X100으로 설정한다. 두 번째 은닉층의 웨이트 매트릭스 W2를 100X10으로 설정한다. 이와 같은 뉴럴 네트워크 구조에 대해서 NumPy 어레이 형태로 다음과 같이 입력 x, 출력 y, 2개의 은닉층에 대한 웨이트 매트릭스를 각각 w1, w2 로 프로그램하고 랜덤 수로 초기화 하자.

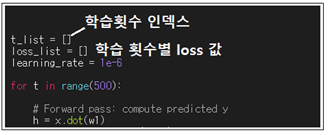
learning rate 은 1e-6 으로 설정하다. 이 보다 크면 발산해 버린다. 이 코드에서 학습 횟수는 500회로 설정하며 t는 0에서 499까지 나타내는 인덱스로서 마지막 그래프 작성 과종에서 가로축 변수로 사용한다. loop 내에서 그때그때 리스트형 데이터로 t 값을 append 해 둔다. 동시에 loss 값도 별도로 append 하여 loss 값 변화를 작도하도록 한다.

은닉층(hidden layer)이 2개이므로 상호 독립적인 웨이트 매트릭스도 w1, w2 2개이다. Backpropagation을 계산하기 위해서는 loss 함수를 w1과 w2 에 대해 편미분할 필요가 있다. w2에 대해서는 쉽게 편미분이 가능하다. 한편 w1에 관해서는 ReLU 함수에 의한 합성함수이므로 Chain Rule에 의한 합성함수 미분법을 사용해야 한다.

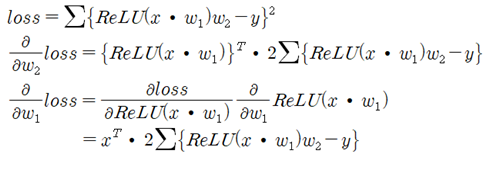
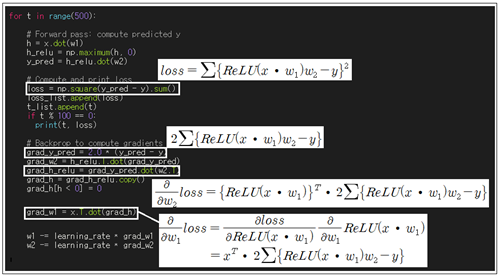
forward pass는 입력 x 에 웨이트 매트릭스 w1을 곱한 후 ReLU 처리한 다음 다시 웨이트 매트릭스 w2를 곱하는 과정이며 그 결과를 제곱하여 합하면 loss 함수가 얻어진다. 만약 계산된 loss 함수 값이 0.0 보다 상당히 커 최소값이라 판단할 수 없으면 웨이트 값들 즉 w1 과 w2 매트릭스의 값들을 업데이트해서 loss 함수 값을 다시 계산해 보아야 한다. 이와 같이 웨이트 값들을 업데이트 하는 과정에서 반드시 편미분 값들을 계산해 낼 필요가 있는데 이를 Backpropagation 이라고 한다.

아래는 500회 학습 과정에서 0.0에 가까이 접근하는 loss 함수 값을 그래프 처리하여 보았다. 아울러 PC의 cpu를 사용한 실행 시간은 1.28초가 소요되었다. 만약 구글 Colabo에서 GPU를 연결하여 계산해 보아도 약 1.0 초가 소요된다. NumPy 라이브러리는 GPU 계산 시간 단축에 적합하지 않다는 점에 유의하자.

NumPy 라이브러리 범 위내에서 작성한 뉴럴 네트워크 코드는 Backporpagation 처리 방식에 있어서 PyTorch 코드와 근본적인 차이점을 보여준다. PyTorch에서도 은닉층별로 속성 파라메터 설정에 의해 Backpropagation 계산을 시키거나 또는 배제시킬 수도 있는 편리한 구조로 되어 있으며 아울러 GPU에 의한 가속계산도 함께 지원하고 있다.

아래에 첨부된 코드는 PyTorch 튜토리얼의 Learning PyTprch with Examples 편 시작부분의 Tensor Warm-up:numpy 코드에 그래프 작도를 위해 약간의 코드를 추가하였다.

#numpy_nn

-- coding: utf-8 --

import numpy as np
import time
import matplotlib.pyplot as plt

start_time = time.time()

N, D_in, H, D_out = 64, 1024, 100, 10

x = np.random.randn(N, D_in)
y = np.random.randn(N, D_out)

w1 = np.random.randn(D_in, H)
w2 = np.random.randn(H, D_out)

t_list = []
loss_list = []
learning_rate = 1e-6

for t in range(500):

# Forward pass: compute predicted y
h = x.dot(w1)
h_relu = np.maximum(h, 0)
y_pred = h_relu.dot(w2)

# Compute and print loss
loss = np.square(y_pred - y).sum()
loss_list.append(loss)
t_list.append(t)
if t % 100 == 0:
  print(t, loss)

# Backprop to compute gradients of w1 and w2 with respect to loss
grad_y_pred = 2.0 * (y_pred - y)
grad_w2 = h_relu.T.dot(grad_y_pred)
grad_h_relu = grad_y_pred.dot(w2.T)
grad_h = grad_h_relu.copy()
grad_h[h < 0] = 0
grad_w1 = x.T.dot(grad_h)


# Update weights
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2

plt.plot(t_list, loss_list)
plt.ylabel('Loss')
plt.xlabel('n')
plt.show()

end_time = time.time()
print( "Completed in ", end_time - start_time , " seconds")

7-21 NumPy 라이브러리에 의한 뉴럴 네트워크 코드의 머신 러닝 특성

-- coding: utf-8 --