2016년 전투바둑으로 세계적으로 유명한 이세돌과 구글 딥마인드의 세기적 바둑 대결이 벌어졌다. 인간의 지능 대 머신 러닝의 대결! 3국까지는 완벽한 머신 러닝의 압승, 4국에서의 예상외 대반전, 예상된 수순이었던 5국으로 끝났다.
4국 후반에서 이세돌 선수의 붙여먹기 포석은 이 대결의 백미를 이룬다. 붙여먹기 전략은 상수가 하수를 상대로 슬쩍 붙여놓고 하수의 대응을 봐서 유리한 국면으로 이끄는 접바둑에서 많이 쓰는 수법인데 구글 딥마인드가 걸려든 듯하다. 구글 딥마인드 자체가 지도학습을 바탕으로 하였기 때문에 바둑 대국 기록을 100% 이상 꿰고 있어야 할 터인데 붙여먹기 학습에 구멍이 있었던 것 같다. 즉 모든 경우의 수를 다 학습했겠지만 하나만 빼먹어도 만약 그 문제가 나오면 틀릴 수밖에 없었던 재미난 대국이었다.
구글 사이트에 바둑을 위한 머신 러닝 라이브러리 GO를 제공하는 듯하다. 하지만 머신 러닝 자체가 오픈 자료가 워낙 많아 따라잡거나 이해하가 불가능할 정도라 여겨지는 것이 사실이지만 Rosenblatt의 퍼셉트론으로부터 시작에서 원론적으로 파다보면 결국 지금의 머신 러닝 전체를 쉽게 조감할 수 있으리라는게 지론이다.
구글 딥마인드의 바둑 알고리듬이 복잡다단하겠지만 결국은 19X19 MNIST 숫자인식 문제와 본질적으로 다를게 없다는 판단이다. 퍼셉트론에서 “+1”과 “-1”로 라벨링 할 수 있었듯이 훈민정음 자음과 모음을 구별하기 위해 Softmax를 적용했던 기법을 통해 바둑 초보자들이 학습하면서 가장 황당해 하는 아다리(호구)라는 것과 1집의 의미를 머신 러닝 예제에 의해서 살펴보자.
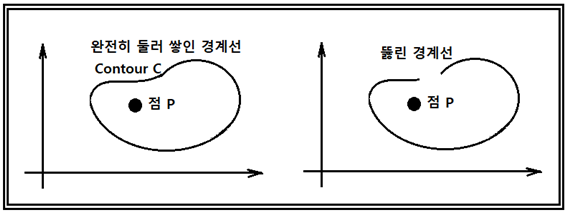
다음의 좌표계는 점 P를 완전히 둘러싼 닫힌 경계선 C와 일부가 뚫린 형태를 각각 보여 주고 있다. 점 P를 흰돌이라 보고 둘러싸는 경계를 흑돌이라 하자.
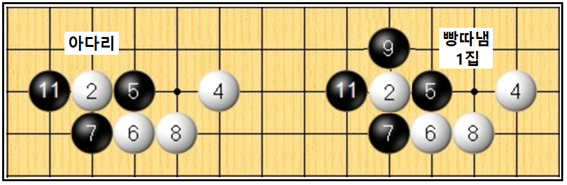
바둑판에서 아다리와 빵따냄 사례를 보자. 백돌 주위 3곳이 흑돌로 막혀 있으면서 한곳으로 뚫려 있는 상태가 아다리 상태이다. 백이 위로 뻗지 않을 경우 흑돌 9번을 두어 2번 백돌을 빵따냄과 동시에 1집이 생기는 것이다.
이 두 상황을 3X3 바둑판에서 구현해 보자. 흑돌, 흰돌 및 바둑판(회색)이다. 흑돌의 픽셀 값은 0.0 흰돌은 1.0 바둑판(회색)은 0.5로 두자. 아다리 경우의 수는 보다 많지만 일단 코드가 제대로 돌아가는지 확인하는 것이 일차 목표이므로 최소한도로 둔다. 만약 부족할 경우에는 라벨 값을 정확하게 산출하지 못할 가능성이 크다는 점을 염두에 두자.
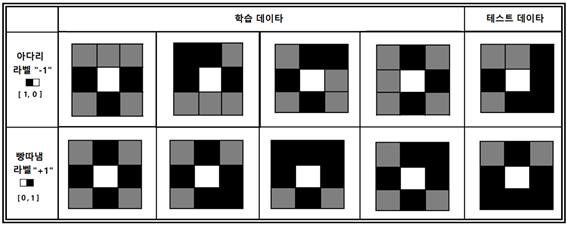
그림을 참조로 해서 아다리 데이터와 빵따냄 데이터를 다음과 같이 작성하자.
아다리⟶ x_data = [[ 0.5, 0.5, 0.5, 0, 1, 0, 0.5, 0, 0.5 ],
[ 0, 0, 0.5, 0, 1, 0, 0.5, 0.5, 0.5 ],
[ 0.5, 0, 0, 0, 1, 0.5, 0.5, 0, 0.5 ],
[ 0.5, 0.5, 0, 0, 1, 0, 0.5, 0, 0 ],
[ 0.5, 0, 0.5, 0, 1, 0, 0.5, 0, 0.5 ],
[ 0.5, 0, 0.5, 0, 1, 0, 0.5, 0, 0 ],
[ 0, 0, 0, 0, 1, 0, 0.5, 0, 0.5 ],
[ 0.5, 0, 0, 0, 1, 0, 0.5, 0, 0.5 ]
]
빵따냄⟶ y_data = [ [1, 0], [1, 0], [1, 0], [1, 0],
[0, 1], [0, 1], [0, 1], [0, 1]
]
이 데이터들은 TensorFlow 코드에서 x_data로 입력하고 one hot code는 y_data로 입력한다.
마지막 칸의 Test 용 데이터는 Session에서 입력하여 아다리인지 빵때림인지 알아보기로 한다.
아다리?⟶[ 0.5, 0.5, 0, 0, 1, 0, 0.5, 0, 0 ]
빵따냄?⟶[ 0.5, 0, 0.5, 0, 1, 0, 0, 0, 0 ]
X의 샘플수는 3개이지만 None으로 하고 각 샘플의 데이터 수는 9 이다.
one hot code를 저장하는 Y는 2개이지만 None으로 하고 각 각각의 데이터 수는 2 이다.
클라스의 수는 라벨의 수에 해당하는 2이다.
웨이트 W는 X의 데이타수 9와 클라스의 수 2에 맞춰 배열을 선언한다.
바이아스 b는 클라스의 수 2로 두자.
다음의 결과는 테스트용 데이터에 대한 softmax 명령에 의한 계산 결과로서 one hot code의 1 위치에 대응하는 지점의 가장 확률값이 높은 hypothesis 값을 보여준다. 그 뒤의 브라켓 속의 값을 살펴보면 학습결과에 맞춰 정확히 인식했음을 알 수 있다. 하지만 아다리 경우의 hypothesis 확률값이 90.7% 로 생각보다 낮은 값을 보여주는데 그 이유는 학습 데이터가 수가 부족해서 그런 것이 아닐까? 빵따냄의 경우는 94.4% 로 적절히 높은 확률값이라 보인다.

거의 퍼셉트론 수준의 머신 러닝 코드에 TensorFlow 의 Softmax를 사용하여 바둑의 아다리 문제를 아다리와 빵때림으로 라벨을 부여하여 분석해본 결과 의외로 좋은 결과를 얻었다. 매번 실행할 때 마다 확률값이 변동될 수 있으나 라벨값 예측에 실수가 없으면 될 것이다.
아래의 코드를 복사해서 실행할 경우 혹 indentation 이 잘못되어 에러가 검출되면 2018년 8월 10일의 indentation 위치 AS 내용을 참조하기 바란다.(마크다운 특성 상 항상 인덴테이션이 사라짐)
#softmax_classifier_9data_atari_Rosenblett_01.py
#Softmax Classifier
from matplotlib import pyplot as plt
import numpy as np
import tensorflow as tf
tf.set_random_seed(777) # for reproducibility
def gen_image(arr):
t_d = np.reshape(arr, (3, 3))
two_d = (np.reshape(arr, (3, 3)) * 255).astype(np.uint8)
print(two_d)
plt.imshow(two_d, interpolation='nearest')
plt.savefig('batch.png')
return plt
x_data = [[ 0.5, 0.5, 0.5, 0, 1, 0, 0.5, 0, 0.5 ],
[ 0, 0, 0.5, 0, 1, 0, 0.5, 0.5, 0.5 ],
[ 0.5, 0, 0, 0, 1, 0.5, 0.5, 0, 0.5 ],
[ 0.5, 0.5, 0, 0, 1, 0, 0.5, 0, 0 ],
[ 0.5, 0, 0.5, 0, 1, 0, 0.5, 0, 0.5 ],
[ 0.5, 0, 0.5, 0, 1, 0, 0.5, 0, 0 ],
[ 0, 0, 0, 0, 1, 0, 0.5, 0, 0.5 ],
[ 0.5, 0, 0, 0, 1, 0, 0.5, 0, 0.5 ]
]
y_data = [ [1, 0], [1, 0], [1, 0], [1, 0],
[0, 1], [0, 1], [0, 1], [0, 1]
]
X = tf.placeholder("float", [None, 9])
Y = tf.placeholder("float", [None, 2])
nb_classes = 2
W = tf.Variable(tf.random_normal([9, nb_classes]), name='weight')
b = tf.Variable(tf.random_normal([nb_classes]), name='bias')
#tf.nn.softmax computes softmax activations
#softmax = exp(logits) / reduce_sum(exp(logits), dim)
hypothesis = tf.nn.softmax(tf.matmul(X, W) + b)
#Cross entropy cost/loss
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis=1))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
#Launch graph
with tf.Session() as sess:
for idx in range(6):
output = x_data[idx]
gen_image(output).show()
sess.run(tf.global_variables_initializer())
for step in range(2001):
sess.run(optimizer, feed_dict={X: x_data, Y: y_data})
if step % 200 == 0:
print(step, sess.run(cost, feed_dict={X: x_data, Y: y_data}))
print('--------------')
# Testing & One-hot encoding
a = sess.run(hypothesis, feed_dict={X: [[ 0.5, 0.5, 0, 0, 1, 0, 0.5, 0, 0 ]]})
print(a, sess.run(tf.argmax(a, 1)))
print('--------------')
bb = sess.run(hypothesis, feed_dict={X: [[ 0.5, 0, 0.5, 0, 1, 0, 0, 0, 0 ]]})
print(bb, sess.run(tf.argmax(bb, 1)))
print('--------------')
all = sess.run(hypothesis, feed_dict={
X: [[ 0.5, 0.5, 0, 0, 1, 0, 0.5, 0, 0],[ 0.5, 0, 0.5, 0, 1, 0, 0, 0, 0]]})
print(all, sess.run(tf.argmax(all, 1)))
아다리와 멍때림 인 줄 알았는데. 바둑 용어였네요. ㅋㅋㅋㅋ 재밌습니다.전에 머신러닝 수업 갔는데 codingart님 글에서 봤던 softmax가 나와서 반갑더라구요. ㅎㅎㅎㅎ
이미 머신 러닝도 해 보셨군요!
아, 아주 조금입니다. ㅋㅋㅋㅋ
신기한 사건이네요
예 softmax가 되게 중요한 함수 중 하나라고 하더군요. 물론 못 알아들었습니다만 ㅋㅋㅋ
아다리 아다리!
pairplay 가 kr-dev 컨텐츠를 응원합니다! :)
이오스 계정이 없다면 마나마인에서 만든 계정생성툴을 사용해보는건 어떨까요?
https://steemit.com/kr/@virus707/2uepul