안녕하세요, 암호화폐가 가져올 새로운 미래를 꿈꾸는 @Cryptodreamers 입니다.

암호화폐 생태계가 안정적으로 운영되기 위해서는 어떻게 설계를 해야 할까요? DApp으로 태어난 기업이 유니콘이 되어 활개를 펼칠 머지 않은 미래에 대해서 큰 꿈을 꾸는 사람들에게 이것은 정말 흥미로운 문제입니다.
성공적인 암호화폐의 생태계를 구축하기 위해서 설계자는 다양한 고민을 해야할 것입니다. 1) 기술적으로 구현된 토큰을 2) 어떻게 사람들이 많이 토큰을 사용하도록 유도할 것이며, 3) 어떻게 지속적으로 암호화폐 생태계가 성장하도록 4) 어떤 방식의 인센티브와 페널티 구조를 설계할 것인가. 이러한 고민들은 수 없이 많은 실제 비지니스 모델의 성패를 통해서 학습되고, 끊임없이 진화하며 결국 풀어나갈 것이라고 믿습니다.
토큰 이코노미의 본질은 끊임없이 살아숨쉬는 하나의 유기적이고 완결성을 지닌 생태계를 구축하는 것입니다. 이 때문에 설계자의 의도대로 생태계가 긍정적인 선순환을 할 수 있도록, 사람들이 특정한 방식의 행동을 하도록 유도할 필요가 있습니다. 인센티브와 페널티로 말이죠.
효과적인 인센티브와 페널티 시스템을 만들기 위해서는 사람들이 주어진 상황에 대해서 어떻게 반응하는지에 대한 이해가 있어야합니다. 즉, 특정한 상황에서 행동방식에 영향을 끼치는 심리적인 요인을 명확히 인식하고 이것을 설명할 수 있는 객관적인 도구들도 필요하겠죠. 이러한 측면에서 토큰 이코노미에 큰 도움을 줄 수 있는 현존하는 심리학적, 수학적, 경제학적 이론으로 게임이론이 있습니다.
게임이론은 1944년 수학자인 폰 노이만(John von Neumann)과 경제학자인 모르겐슈테른(Oskar Morgenstern)이 함께 저술한 "게임이론과 경제행동"에서 나왔습니다. 정확하게 50년 뒤인 1994년, 존 내쉬(John Nash)의 "균형이론"에 의해 발전하였습니다. 존 내쉬는 균형이론이 인류에 기여한 바에 대한 혁혁한 공적을 인정받으며, 노벨 경제학상을 수상하기도 했습니다. 국가간의 정치경제적 협상을 위한 전략으로 활용되기도 하고, 실제로 미국의 핵 전략론으로 활용되기도 했습니다.
게임이론은 사람들이 특정한 상황에서 행동하는 방식에 대해 설명해줄 수 있고, 또 나아가서 그런 행동방식을 어떻게 하면 바람직한 방향으로 유도할 수 있을 것인지에 대한 해결책을 제시해줄 수 있습니다. 토큰 이코노미에서도 네트워크 참여자에 대한 인센티브와 페널티 제도를 설계하고, 설계자가 원하는 방향으로 특정한 행동을 유도하기 위해서 게임이론을 충분히 이해할 필요가 있습니다. 이번 포스팅에서는 게임이론에 대해서 알아보겠습니다.
1. 게임이론이란?
조직을 위한 시스템을 디자인할 때, 결국 목표는 사회적 질서와 긍정적인 결과를 도출하기 위해 어떻게 사람들의 상호작용을 이끌어낼 것인가에 대한 것들입니다. 그래서 사람들을 위한 시스템을 구축할 때 심리적인 접근 방식이 필요합니다.
아주 감사하게도 몇 십년전에 경제학자들이 정확하게 이 목적을 위해서 연구해온 분야가 잇습니다. 덕분에 사람들이 특정한 상황에서 어떻게 행동하는가에 대해서 수학적, 경제적 분석을 할 수가 있죠.
게임이론은 사람과 동물, 심지어 컴퓨터가 이성적인 결정을 하는 것에 대해 설명해줄 수 있는 이론입니다. 몇 가지 활용사례를 보겠습니다.
- 정치학에서 상대국이 어떻게 행동할 것인지에 대해 연구할 때 활용
- 전쟁에서 적의 행동을 예측하기 위해서 활용
- 암호학에서 잠재적인 사이버테러를 예측하고 선제대응 하기 위해 활용
- 금융시장에서는 주식시장의 움직임을 예측할 때 활용
- 토큰 이코노미에서는 설계된 인센티브 시스템에 대해서 토큰의 보유자들이 어떤 행동을 취할 것인지에 대해서 예측할 때 활용
이러한 예측들은 사람들이 이성적인 행동을 하기때문에, 자신의 이익을 극대화하고 동시에 손실을 최소화하려는 경향이 있다는 전제에 근거합니다. 그렇기 때문에 계산할 수 있는 것이죠. 즉, "게임"에서 플레이어가 어떻게 행동할 것인지를 안다면 그 결과를 통제할 수 있습니다. 이렇게 만들어진 결과를 통제하는 것을 게임이론에서는 지배전략(dominant strategy)라고 표현하고, 이 전략을 활용해서 사람들이 하는 행동에 대해서 예측할 수 있습니다.
2. 게임이론을 어떻게 활용하는가?
죄수의 딜레마(Prisoners' dillema) 상황 , 핵 전략(Nuclear welfare) 상황, 노사관계 (labor relation) 상황 등에 활용할 수 있습니다. 실제로 미국과 소련간의 냉전시대에 핵 전쟁위험에 대비하기 위해 미국에서 활용했던 핵 전략을 예시로 한 번 살펴보겠습니다.
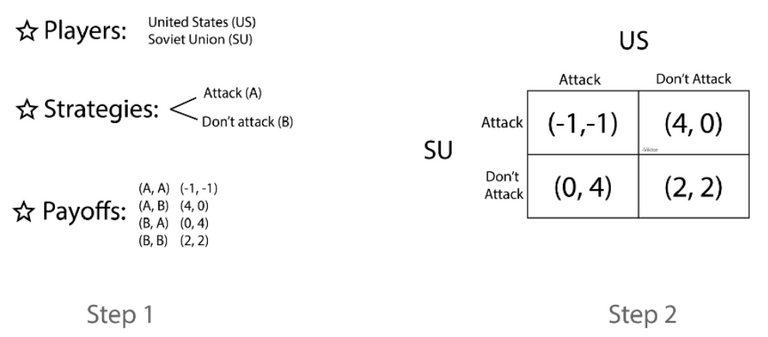
특정한 상황이 게임으로 규정되고, 분석되기 위해서 몇 가지 조건들이 필요합니다.
- 참가자(players), 전략(strategies), 행동의선택에 따른 비용(혹은 효용 : payoff)
- 게임의 형태 (어떠한 형태의 게임인지 : 협조적 게임상황인지 혹은 비협조적 게임상황인지, 반복적인 게임인지 아닌지)
또, 비용(payoff)이라는 것은 때때로 다른 의미를 갖기도 합니다. 만족이나 개인의 효용으로 쓰이기도 합니다. 한 개인이 받는 금전적인 보상을 의미하기도 합니다. 특정한 상황에서 제공되는 금전적 보상 및 효욕의 기대치를 의미하기도 합니다. (Payoff를 비용이나 효용을 정량화한 수치로 이해하시면 될 것 같습니다.)
미국과 소련의 상호작용에 대한 결과를 예측하기 위해서 내쉬의 균형 게임이론이 필요합니다.
내쉬의 균형이론(Equilibrium)
내쉬의 균형이론은 각각의 당사자들이 다른 사람의 행동에 대해서 자신의 행동을 바꿀 인센티브가 없는 상황에서 나오는 결과입니다.
내쉬의 균형이론에서 계산을 하는 방식은 다음과 같습니다. Payoff(비용,효용)은 US(United States)가 먼저고 SU(Soviet Union)가 두 번째 입니다. 이런 방식으로 표현이 되겠죠. (United States payoff, Soviet Union payoff). 이하의 그림을 통해 한 번 살펴보겠습니다.
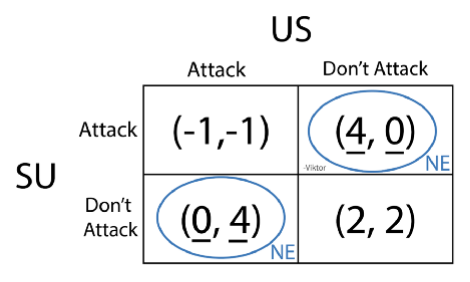
- (좌측 상단) 미국이 공격했을 때 미국의 Payoff를 먼저 한 번 보세요. -1보다는 0이 낫기 때문에 0에 밑줄
- (우측상단) 미국이 공격을 하지 않을 때 미국의 Payoff를 먼저 한 번 보세요. 4와 2가 있습니다. 4가 낫기 때문에 4에 밑줄
- (좌측하단) 소련이 공격했을 때 소련의 Payoff를 먼저 한 번 보세요. 01보다는 0이 낫기 때문에 0에 밑줄
- (우측하단) 소련이 공격을 하지 않을 때 소련의 Payoff를 먼저 한 번 보세요. 4와 2가 있습니다. 4가 낫기 때문에 4에 밑줄
이 게임에서의 지배전략(Dominant strategy)은 (공격하기, 공격하지 않기) 혹은 (공격하지 않기, 공격하기)입니다.
3. 게임의 분류시 고려사항들
게임을 고려할 때, 이하와 같은 고려를 통해 분류할 수 있습니다.
- 3.1 모든 당사자들은 같은 완전하고 동등한 정보를 갖고 있는가?
- 3.2 당사자간의 이익이 상대방과 완전히 상충되는가? 아니면 공동선이 있는가?
- 3.3 협력하도록 합의하는 것이 강제될 수 있는 상황인가?
- 3.4 게임의 과정들이 동시에 발생하는가? 아니면 인과관계를 갖고 발생하는가?
- 3.5 게임이 같은 상대를 대상으로 반복적으로 발생하는가? 아니면 상대방이 바뀌는가?
하나씩 살펴보겠습니다.
3.1 모든 당사자들은 같은 완전하고 동등한 정보를 갖고 있는가?
불확실 정보(Imperfect information) VS 확실한 정보(Perfect information)
불확실한 정보는 게임의 상황에서 외부적인 불확실성을 갖고 있을 때(날씨나 상품의 퀄리티같은 외부적인 요인에 대한 불확정성이죠) 혹은 전략적 불확실성(각각의 당사자들이 상대방이 예전과 동일한 방식으로 행동할지 혹은 다른 방식으로 행동할지에 대해서 확신할 수 없는 상황)이 있을 때 존재합니다.
불완전 정보(Incomplete information) VS 완전 정보(Complete information)
미완결 정보는 한 당사자가 다른 사람들에 비해서 더 잘 알때 발생합니다. 정보 비대칭이 있는 상황이죠. 이러한 상황에서는 당사자는 추측하거나 숨기거나 혹은 그들이 가진 사적인 정보가 게임의 중요한 요소가 됩니다. 완결된 정보는 이와 반대로 모든 사람들이 완전하고 동등한 정보를 갖고 있는 상황이죠.
3.2 당사자간의 이익이 상대방과 완전하게 상충되는가? 아니면 공동선이 있는가?
게임의 기본
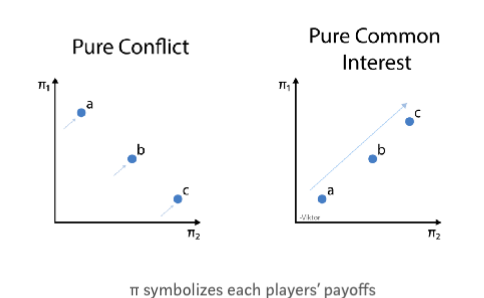
순수한 갈등(Pure conflict)과 순수한 일반 갈등(Pure common conflict)가 있습니다. 예를 들어, 도로의 교통상황이 좋지 않을 때는 공통의 이익을 갖고 있는 상황이라 할 수 있습니다. 교통이 막히면 모두가 빨리 갈 수 없고, 모두에게 이익을 줄 수 있는 것은 불가능합니다. 또 다른 상황은 물건을 교환할 때의 가격을 결정하는 협상이나 제로섬 게임같은 것들도 있습니다. 즉, 누군가가 이득을 취하면 누군가는 그에 대한 이익을 잃는 것이죠. 이러한 것들이 갈등의 예라고 할 수 있습니다.
공유지의 비극(Tragedy of commons)
대부분의 게임에서는 공통의 이익과 갈등의 요소를 모두 갖고 있습니다. 공유지의 비극은 공급을 초과하는 개인의 내쉬 균형을 가지는 일반적인 문제라고 할 수 있습니다. 또, 한 개인의 이익을 위해서 많은 목초를 소비하게 되면 다른 사람에게 즉각적인 피해를 끼치게 되는 상황이죠. 이 문제는 특정한 자원이 당사자들에게 무료로 제공되는 게임에서 발생하곤 합니다. 이러한 결과로 이하와 같은 상황들이발생할 수 있습니다.
- 남획 (사냥·어업 등에서 자원량의 변동에 영향을 미칠 정도로 많이 잡는 일)
- 대기오염
- 공공의 목초지가 보존되지 않는 현상
- 국도에서 발생하는 교통혼잡
- 기하급수적인 인구의 증가
- LA에서의 지하수 부족현상
- 바다의 쓰레기 문제
게임의 기본적 분류
당사자들의 이익이 서로 완전한 갈등인 빚는 상황(제로섬같은 경우)이거나 혹은 공동의 선이 있는 경우에 게임을 분류하는 가장 기본적인 분류법입니다. 몇몇 상황들을 분류하는데 도움이 될 수 있습니다.
- 보이지 않는 손의 게임(Invisible Hand games) : 각자의 이익을 위해 움직일 때 모두에게 이익이 되는 상황
- 죄수의 딜레마(Prisoner’s Dilemma) : 상대방을 신뢰할 수 없고, 상대방의 선택을 알 수 없는 상황
- 순수한 동등한 게임(Pure Coordination games) : 서로 같은 활동을 하면 서로 같은 이익을 취하는 상황
- 확정 게임(Assurance games) : 죄수의 딜레마와 비슷한 상황으로 사슴 사냥(stag hunt)으로 표현되기도 합니다. 상대방과의 협동을 통해 이익을 볼 수 있지만 상대방의 선택을 알 수 없는 상황.
- 성별의 갈등(Battle of sexes) : 서로 같은 활동을 하길 선호하지만 서로의 역할이 달라서 누군가가 더 큰 이득을 취하는 상황
- 매-비둘기 게임(Hawk-Dove) : 도킨스의 이기적 유전자에 나온 사례로, 항상 치열하게 싸우는 매와 적당히 도망가는 비둘기가 존재. 상대방과 경쟁해야하는 상황
- 치킨 게임(Chicken Games) : 자동차를 탄 상태에서 벽을 향해서 죽기 전 혹은 상대방이 포기할 때 까지 돌진하고 벽에 가깝게 정차한 자가 승리하는 게임 상황
3.3 합의를 통해 상대방에게 의무를 강요할 수 있는 상황인가?
협동게임(Cooperative game)과 비협동게임(Non-Cooperative game)
먼저 협동게임입니다. 서로의 의사결정이 상대방에게 영향을 끼치는 상황을 생각해보세요. 참여자의 행동은 서로 영향을 줄 수 있고, 어떤 참여자도 비용없이 강제할 수 있는 협약에 제약되기 쉬운 상황입니다. (서로의 의무에 대해 상세하게 명시해놓은 계약서를 통해서 성립한 노사관계를 생각하시면 됩니다.) 이러한 상황을 협동적인 게임이라고 할 수 있습니다. 이 용어는 상대방에 대해 협동적인 태도나 감정을 언급하는데 사용하는 것이 아니라, 서로의 상호작용에 있어 제도적인 방법을 통해서 통제할 수 있다는 의미입니다.
이와 상반되게 비협동적 게임 상황은 좀 더 일반적으로 어떤 교류에 있어 강제할 수 있는 제한을 할 수 없는 상황입니다. 이러한 상황을 비협동적 게임 상황이라고 합니다. 여기서 나오는 협동적, 비협동적이라는 단어의 의미는 협동을 하겠다 혹은 하지 않겠다는 의도를 말하는 것이 아니라, 상대방에 대한 제도적인 방식으로 강제할 수 있는 수준을 언급하기 위한 것입니다.
고용자와 피고용인과 같은 사회적 관계에서는 상호작용의 방식이 협조적인 방식이 될 것입니다. 왜냐하면 고용자와 고용인은 임금과 근로시간 등을 협상할 수 있기 때문입니다. 이 상황에 존재하는 또 다른 측면은 계약과 관련된 것과 기록된 것 이외의 비협조적인 부분이 될 것 입니다.
근로자가 얼마나 열심히 일하는가, 혹은 고용자가 회사의 이익을 얼마나 다시 회사에 투자하는가 등의 예시가 있겠죠. 고용자가 생산성을 측정할 때 출입문에 출입을 체크하는 기계를 설치하고, 근로자가 사무실을 나갔다 들어왔다 할 때마다 확인을 하고 이를 통해 생산성을 측정한다면 협조적인 방식이라고 할 수 있습니다. 만약 이런 방식이 아니라 고용자가 근로자의 작업의 질이나 노력을 측정할 수 없다면 비협조적 상태라고 할 수 있겠습니다.
특히 스타트업같은 기술근로직에서는 근로자의 생산성을 측정하는 것이 매우 어렵습니다. 그렇기 때문에 대부분 비협조적 상황이 됩니다. 이는 소위 사내문화라고 불리는 것과 회사의 미션에 대해서 근로자들이 자주 듣는 이유이기도 합니다. 고용자들은 특정한 방식의 강제할 수 있는 협약이 존재하지 않을때, 이성적인 근로자들은 계약서에 명시된 문제를 일으키지 않고, 근무에 대해서 해이해질 수 있습니다. 그래서 사내에서 존재하는 '문화'의 이야기들은 만들어져있는 사회적 계약을 각인시키기 위한 것이죠.
일반적으로 특정한 관계가 협조적인지 비협조적인지 혹은 게임의 비용(payoff)가 공통의 선이 있는지 아니면 갈등관계인지에 근거해서 사회적 교류가 분류됩니다.
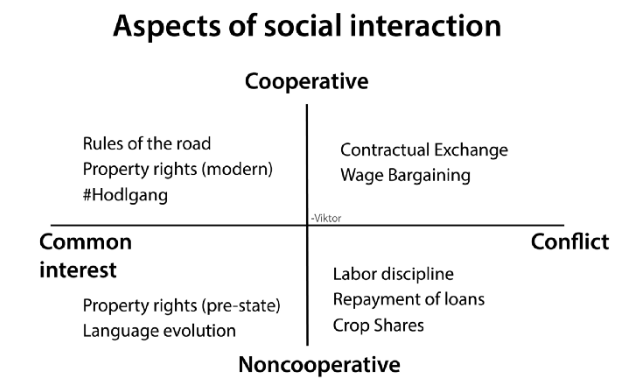
3.4 게임의 과정들이 동시에 발생하는가? 아니면 인과관계를 갖고 발생하는가?
순서의 결정을 판단하는 두 가지 주요한 게임이 있습니다. 보통형태의 게임(Normal Form Games)과 확장된 형태의 게임(Extensive Form Games)입니다.
보통형태의 게임(Normal Form game)
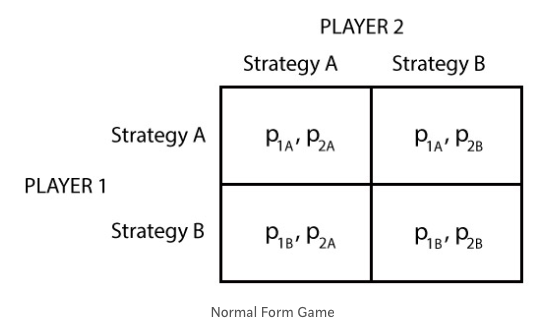
이 의미는 각각의 당사자들이 행동을 하는 인과관계가 명확하지 않을 때, 상대방의 선택에 대한 정확한 정보없이 추측이 이루어질 때를 말합니다. 이런 게임에서는 당사자들이 동시에 행동한다고 생각하기 때문에, 행동의 선택으로 인한 결과는 중요하지 않습니다.
연장된 형태의 게임(Extensive Form game)
연장된 형태의 게임에서는 행동의 순서가 명확하고, 당사자들은 게임의 어느 단계에 있는지 정확하게 알고 있습니다. 이전에 선택했던 행동들은 이후에 선택하고 행동하는 당사자들이 인지할 필요가 없죠.
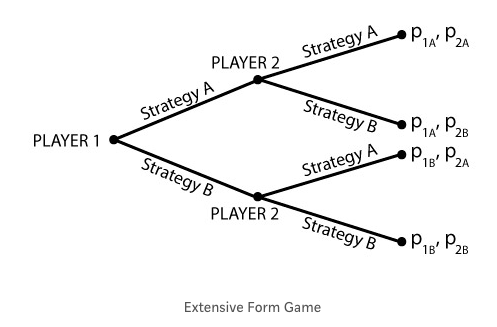
연장된 형태의 게임은 많은 면에서 상호교류에 대한 정보를 전달합니다. 그래서 연장된 형태의 게임은 일반적인 형태의 게임과 동일하다고 비춰질 수도 있습니다. 보통 형태의 게임이 활용되는 일반적인 상황에서, 연장된 형태의 게임에 있는 추가적인 정보는 그들이 게임을 어떻게 진행할 것인지에 대해서 무관하다고 생각하기 때문입니다.
3.5 게임이 같은 상대를 대상으로 반복적으로 발생하는가? 아니면 상대방이 바뀌는가?
반복적인 게임은 연장된 형태의 게임이 여러번 반복적으로 구성되어 있는 것입니다. 반복된 게임은 당사자가 자신의 현재 행동의 영향에 대해서 고려해야하고, 상대방의 미래 행동에 대해서 예측해야하는 상황을 이야기하는 부분이죠.
반복된 게임은 사회적 질서에서 가장 강력한 수단이기도 합니다.
반복된 게임은 어떻게 죄수의 딜레마가 시스템의 디자인으로 극복될 수 있는지(죄수의 딜레마를 반복하면 딜레마가 해결되기도 합니다), 국가간에 전쟁의 위기를 조장하는 것이 큰 비용이 드는 일인지(전쟁위기를 조장하는 것은 단기적으로는 크게 이익이 되죠), 그리고 어떻게 때때로 군주제가 꽤 잘 운영될 수 있는지 등에 대해서 설명해 줄 수 있습니다.
마무리

세기의 명작, 영화 매트릭스에 주인공 네오가 만난 매트릭스의 아키텍트는 인간세계의 모든 경우의 수와 모든 가능성을 매트릭스에 담아내려고 했습니다. 하지만 인간의 본성이 때때로 비이성적이며 충동적이고, 사랑이라는 감정에 예상할 수 없는 선택을 하는 특성을 가졌기 때문에 그는 매트릭스를 현실 그 자체로 만들어내지는 못한다고 고백했었죠. 결국 설계에 있어 모든 변수를 완벽하게 고려하기는 매우 힘들다는 결론입니다.
(적어도 우리는 매트릭스를 설계하는 것이 아니기에) 암호화폐 생태계를 구축함에 있어서, 생태계의 구성원들에게 존재하는 많은 변수들이 있을지라도, 이러한 가능성들을 잘 관리하도록 설계한다면 큰 방향성은 결국 생태계 성장에 도움이 되는 상호이익을 추구하는 공생관계로 창조할 수 있지 않을까요? 제2의 스팀, 제3의 스팀 그리고 이러한 생태계의 성장을 통해 생태계 참여자의 모두가 이익을 누릴 수 있는 플랫폼도 곧 나오지 않을지 기대를 해봅니다.
이런 상황에서 게임이론과 앞으로 더 깊게 연구될 분야들은 이러한 생태계의 구축에 큰 도움을 줄 수 있을 것이라 생각합니다. 게임이론은 상황에 대한 인간의 선택과 관련한 해석과 해결방안을 제시해줄 수 있기 때문입니다.
게임 소개
게임이론을 플래쉬 게임으로 잘 구현 해놓은 페이지가 있어 마지막으로 소개를 하려 합니다.
이 게임에서는 상대방의 선택을 알 수 없는 상황에서, 두 명의 플레이어가 슬롯머신에 코인을 1개씩 넣는 게임을 진행합니다. 룰은 간단합니다. 게임 후 코인 갯수의 변화를 이렇게 표시할게요 (나, 상대방). 슬롯머신에 넣은 코인 1개는 반환되지 않습니다.
- 상대방이 머신에 코인을 1개 넣고, 나도 1개를 넣으면 서로 2개를 얻습니다. (+1, +1)
- 상대방이 머신에 코인을 1개 넣고, 나는 넣지 않으면 나만 3개를 얻습니다. (+2, -1)
- 상대방이 머신에 코인을 넣지않고, 나는 1개를 넣으면 상대방만 코인을 3개 얻습니다. (-1, +2)
- 상대방과 나도 코인을 넣지않으면, 아무일도 일어나지 않습니다. (0, 0)
이 게임을 반복적으로 한 사람과 5번을 시행합니다. 1:1의 상황은 다소 간단합니다.
만약에 참여자가 30명이고 1:1게임을 토너먼트 형식으로 순차적으로 진행한다면 어떻게 될까요? 참여자의 수가 사회 전체의 규모로 커진다면 어떻게 될까요? 플래쉬게임을 한 번 해보신다면, 흥미로운 결과를 발견하실 수 있을 것 같습니다 :D
게임이론을 실제로 체험해볼 수 있는 플래쉬 게임
http://ncase.me/trust/
Reference
Game theory
https://en.wikipedia.org/wiki/Game_theory
Coordination game wikipedia
https://en.wikipedia.org/wiki/Coordination_game
Battle of sexes wikipedia
https://en.wikipedia.org/wiki/Battle_of_the_sexes_(game_theory)
Stag hunt wikipedia
https://en.wikipedia.org/wiki/Stag_hunt
Extensive form game wikipedia
https://en.wikipedia.org/wiki/Extensive-form_game
Cryptoeconomy - game theory
https://medium.com/blockchannel/cryptoeconomic-theory-game-theory-basics-fb3a49aab1a8
Useful, thanks
Thx a lot!
양질의 글 감사합니다
감사합니다 스윗포테이토님^^!
Congratulations @cryptodreamers! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP@홍보해
방문해주셔서 감사합니다 송가님~
팔로우하고 재밌는 글보러 종종 들리겠습니다.ㅎㅎ
감사합니다^^
댕댕이 너무 귀엽네요...
잘 보았습니다. 해박한 지식과 적절한 비유가 좋네요.
한꺼번에 다 이해가 안 되어
팔로우하고 틈틈이 배우겠습니다
고맙습니다
방문해주셔서 감사합니다^^
자주 뵙겠습니다.ㅎㅎ
저도 게임이론 관련 책 한권을 본적이 있는데 잼있더라고요
잘보고 갑니다~
안녕하세요~! 방문해주셔서 감사합니다^^
양질의 글 발견...! 저랑같은 crypto글을 보면 매우반가운 생각이 드네요 ㅜㅜ 저도 드리머를 꿈꾸는 자로서 더 좋은 글을 싣도록 노력해봐야겠네요 . 보팅하고 팔로우할게요 :))
감사합니다^^
자주 뵈어요!
와!!!! 이건 완전 논문 수준입니다!!! 저가 올리는 글하고 하늘과 땅 차이네요!! 읽어도 잘 모르겠지만 수준 높은 글이라는것은 알겠네요 ㅎㅎㅎ
제가 코인들의 fundamental 약해서..
"내쉬의 균형이론" 을 특히 재미있게 읽었습니다.
계속 수준 높은글 올려주시길!
응원해주셔서 감사합니다! 화이팅하겠습니다~
좋은 하루 되세요!
와....수준급 글 감사합니다!
지금은 슬쩍 훑어봤는데, 나중에 시간 날 때 자리 잡고 찬찬히 읽어야겠어요!
방문해주셔서 감사합니다^^