K-mooc 인공지능과 기계학습 강의를 듣고 정리해봤어요 ;) 인공지능은 공부하면 할수록 참 재미있습니다.
- 확률론(Probability)
- 키워드 정리: 조건부확률, 사전확률, 사후확률, Bayes Rules, Joint Probability
*조건부확률(Conditional Probability): 조건이 주어졌을때 사건이 일어날 확률을 알고싶은것
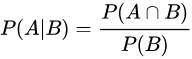
P(X = x | Y = y) =
=? 조건
random variable
*결합확률(Joint Probability): 두개의 서로다른 사건이 동시에 일어나는 확률을 말한다.
동전으로 치면 동전 2개를 동시에 던지는 것이다.
{0,0}, {0,1}, {1,0}, {1,1} 의 경우가 나오므로
모든 joint probability는 1/4가 된다.
*사전확률(Prior Probability): 알고있는 확률 예를들어, A상자에 흰공이 7개 검은공이 3개 들어있다면 A상자에서 흰공을 뽑을 확률 P(A) = 7/10이다. 이런 확률을 사전확률이라한다.
*사후확률(Posterior Probability): 사후 확률이란 우리가 A, B 각 상자에서 공을 선택하는 확률이 사전에 정해져있다. 다만 관찰된 공들이 어느 상자에서 나왔는지 알아내는 것이 바로 사후확률이다. 즉 P(A|흰공), P(B|흰공)의 경우는 흰공이 주어지고 나서 주머니에서 A, B를 선택하는 확률을 의미한다. 즉 P(X=A|Y=흰공) Y사건이 일어난 뒤에 X에 따라 확률을 따지는 것이기 때문에 사후확률이라 한다.
*베이즈 정리(Bayes Rule): 결합확률과 곱의 규칙에 따라 베이즈 정리는 아래와 같이 유도가 된다.
P(A|B)=P(A∩B)/P(B)
P(A∩B)=P(A|B)×P(B)
일반적인 조건부 확률 식을 분자 기준으로 풀면 아래와 같다.
P(B|A)=P(A∩B)/P(A)
P(A∩B)=P(B|A)×P(A)
마찬가지로 A에 대한 조건부 확률 B도 이와 같이 표현할 수 있다.
따라서 P(A|B)⋅P(B)=P(B|A)⋅P(A) 로 정의가 되며 이를
P(A|B)=P(A∩B)/P(B) 로 표현 할 수 있다.
따라서 베이즈 룰이 아래와 같이 도출된다.
P(A|B)=P(B|A)⋅P(A)P(B)
이를 바꿔 쓰면 아래처럼 된다.
P(X)P(Y|X)=P(Y)P(X|Y) ⟶ P(X)P(Y|X)P(Y) =P(X|Y)
위에서 확률의 사건 요소별로 정의한 것은 X ∈ {A,B} 와 Y ∈ {흰공,파란공}으로 나타낼 수 있다고 했다.
주머니에서 A와 B를 뽑는다고 하였을 때 아래처럼 기술할 수 있다.
P(Y=흰공or파란공)=P(흰공or파란공|A)P(A)+ P(흰공or파란공|B)P(B)
= P(Y)=P(Y|A)P(A)+ P(Y|B)P(B)
A , B를 X의 요소로 보면 최종적으로 아래처럼 표현 가능하다.
P(Y)=∑P(Y|X)P(X)
Bayes rule을 써서 조건부확률을 joint probability로 만들면
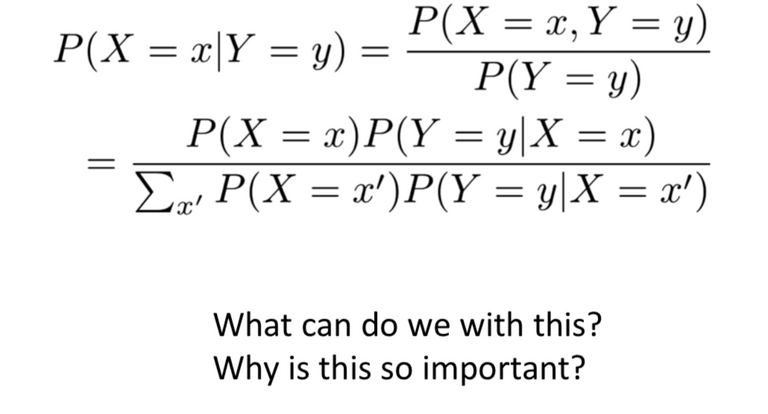
- 문제 정리(Quiz)


일반적으로 비올 확률 Pr(Y=1) = 0.2다. 비가 오던지 안오던지 구름이 낄 확률은 Pr(X=1|Y=1) + Pr(X=1|Y=0)이 된다. 그럼 구름이 낄 확률 Pr(X=1)은 0.24가 되어 구름이 꼈을 때 비가 올 확률을 구하면 2/3이 된다.
모래요정 바람돌이가 하루에 한가지 소원만을 들어주는것처럼
짱짱맨도 1일 1회 보팅을 최선으로 합니다.
부타케어~ 1일 1회~~
너무 밀려서 바쁩니다!!
짱짱맨 화이팅~~