안녕하세요. 대기과학/지구과학 분야의 포스팅을 하고 있는 @hkkim1030입니다.
[오기 전에 알아두자] 태풍 '노루' 경로 분석하기에서,
@hunhani님으로부터, 태풍 경로에 영향을 미치는 인자인
'제트류', '해수면 온도 경도', '몬순 기압골'에 대한 포스팅을 요청 받았습니다.
오늘은, 이것을 설명하기 위한 몇 가지 수학적 기법들에 대한 설명을 해보고자 합니다.
먼저, 
(del operater)입니다.
삼각형을 뒤집어 놓은것 처럼 생긴 이 친구는,
수학공식이 나오는 곳이라면 안쓰이는 곳이 없을 정도로 많이 쓰이는 대단한 친구입니다.
이친구를 정의해 보면,
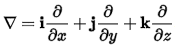입니다.
여기에서, i, j, k는 x, y, z로 표현되는 3차원 공간의 단위벡터 입니다.
쉽게 표현하자만, 는 기울기를 의미하는 기호라고 말 할 수 있습니다.
만약, 에 기압 (P)을 넣는다면
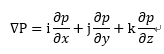
3차원공간에서 기압의 기울기를 의미한다고 보시면 됩니다.
만약 저 공식에 피사의 사탑을 넣는 다면, 탑의 기울기를 구할 수 있겠죠..^^
다음은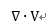 
(divergence)입니다.
여기에서, V는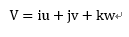 
으로
3차원 공간에서 바람의 속도를 의미합니다.
중간과정을 생략하고 divergence는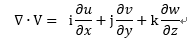 
인데,
만약, v=0, w=0이라고 가정하면
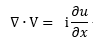만 남게됩니다.
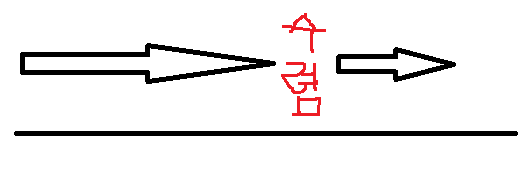
만약, 아래와 같이 x축 방향으로 바람이 점점 빨라진다면,
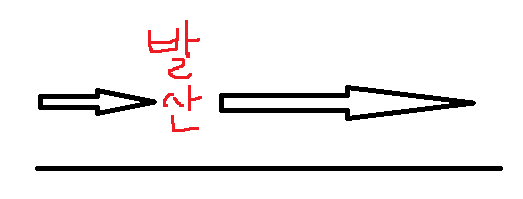
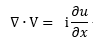가 0보다 커지므로, 우리는 이것을 divergence(발산)으로 정의합니다. (공기가 빠져나갑니다).
반대로, 아래와 같이 x축 방향으로 바람이 점점 느려진다면,
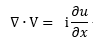가 0보다 작아지므로,
우리는 이것을 발산의 반대인 수렴으로 정의합니다. (공기가 모입니다).
오늘 포스팅은 이 두 가지를 알아보는 것으로 마치겠습니다.
다음편에서는 이 두 가지 공식을 응용하여,
Lagrangian frame과 Eulerian frame에 대한 포스팅을 해보도록 하겠습니다.
좋은 하루 보내시길 바랍니다.
awesome
thanks for your reply.
can u understand korean?
if i get the chance, i will write english version posting
그림이 멋지네요~ㅎㅎ
그림판으로 그렸엌ㅋ
다음엔 툴로 그려야겟다 ㅎㅎ
오 저런 수식 하면 vector identity 들이 막 머릿속에 떠오르는데 저만 그런걸까요? ㅎㅎ
저두여!!!막막 설명해버리고 싶은데 ㅠ
기초부터 하나씩 해보려고요..
누군가에겐 도움이 되겟죠!!ㅎㅎ
그림판 작업 ㅎㅎㅎ 벡터 미적분학이 새록새록 떠오릅니다
여기에서 그림을 그리는게 너무 어려워요!!
워드나 파워포인트면 잘 그리겠는데..ㅠㅠ