Introduction
오늘은 Group의 예시들을 몇가지 살펴보려 합니다. 사실 수학은 예시를 통해서 공부하는 것이 가장 좋습니다. 추상적인 정의들을 알고 있어도 구체적으로 써먹지 못하면 문제 푸는데 아무 소용이 없거든요. 그래서 예시를 풍부하게 알고 있는 것이 도움이 됩니다.
읽기 전에
ℂℕℙℚℝℤ⊕∏∑∅
특수문자들을 몇개 써봤는데 혹시 깨져서 보인다거나 하면 저에게 알려주세요. 갤노트3(ㅠㅠ)으로 보니까 그냥 네모상자로 보이네요. 혹시 다른 모바일 기기에서도 안보일 수 있으니깐..
우선, 본론으로 들어가기 전에 저번 시간에 배웠던 Group의 정의를 복습하겠습니다:
Recall (Definition of a Group)

Examples:
1. (ℤ,+)
저번 시간에 ℤ 를 모든 정수들의 집합으로 정의했었습니다 (ℤ: The set of integers).
정수+정수=정수 니까 +는 ℤ 위에서 binary operation(이항연산)이 되죠
모든 정수 n에 대하여 0+n=n+0=n 입니다. 0은 정수이구요. (항등원의 존재성)
n+(-n)=(-n)+n=0 입니다. -n은 마찬가지로 정수가 됩니다. (역원의 존재성)
결합법칙은 당연히 성립합니다.
따라서 (ℤ,+)는 Group이 됩니다.
Remark
참고로 Group (ℤ,+) 가 한가지 성질을 더 만족시키는 것을 알 수 있는데 바로 교환법칙(Commutativity) 입니다:
a+b=b+a ∀a,b∈ℤ
Group 들 중에서 주어진 이항연산에 대하여 교환법칙(Commutativity)을 만족하는 것을 우리는 abelian Group 이라고 부릅니다. 그러면 (ℤ,+)는 abelian Group이 되겠네요.
2. (ℤ/nℤ,+ mod n)
수학 올림피아드 준비해보신 분들은 Modular Arithmetic 을 공부해보셨을 거에요. 예를 들어
7≡2 (mod 5)
같은 식들을 보셨을 건데 이게 무슨 의미냐면, 7과 2를 5로 나눈 나머지가 같다는 말이에요. (또는 7-2가 5으로 나누어 떨어진다는 말과 동치)
일반적으로, 정수 a,b,n 에 대하여 a≡b (mod n)을 다음과 같이 정의할 수 있습니다:
Definition
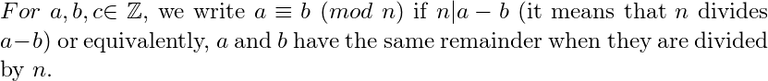
그러면 이렇게 정의한 ≡ (mod n)이 ℤ 위에서 equivalence relation 이 되는 것을 알 수 있구요 , 따라서 ℤ를 ≡ (mod n) 로 quotient 할 수 있습니다. 이 quotient 된 set을 ℤ/nℤ 라고 쓰기로 약속합시다.
무슨 말인지 모르겠다구요? 예시를 들어봅니다. (수학은 모르겠으면 무조건 예시! 100번 강조입니다)
n=5 라고 합시다. 어떤 정수를 5로 나누었을 때 나머지가 뭐가 나오죠? 초등학교 때 배운 나머지정리 (Remainder Theorem)을 아신다면 나머지는 0,1,2,3,4 중 하나라는 것을 알 수 있어요. (5보다 작아야 하니까)
다시 말해서 모든 정수는 5로 나누었을 때 0,1,2,3,4 이 다섯가지 경우로 다 분류할 수 있다는 말이에요:
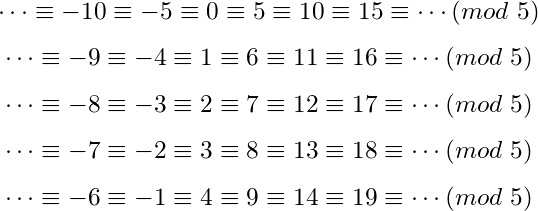
따라서 ℤ/5ℤ={0,1,2,3,4} 가 됩니다.
더 나아가서, ℤ/5ℤ 위에서 연산을 할 수 있죠. 예를들어, 1+3=4 처럼요.
하지만 2+4=6 같은 경우는 6∉ℤ/5ℤ 이기 때문에 +는 ℤ/5ℤ 위에서 이항연산이 아니에요.
이 문제점을 해결하기 위해 덧셈을 하고 mod 5를 해주는 트릭을 쓸 수 있죠. 그러면
2+4=6≡1 (mod 5)
이 되고 1∈ℤ/5ℤ 이 되어 문제가 해결됩니다. 이러한 연산을 modular arithmetic 이라고 합니다.
자, 그럼 위에서 정의된 덧셈 + (mod 5) 에 대하여 ℤ/5ℤ는 Group이 됩니다:
+ (mod 5) 는 위에서 보셨다시피 ℤ/5ℤ 위에서 이항연산이 됩니다.
결합법칙은 당연히 성립합니다.
항등원은 0이죠.
역원은 각각의 원소 0,1,2,3,4 들에 대하여 독자 여러분이 직접 해보세요.ex. 1+4=4+1=0 (mod 5) 라서 1의 + (mod 5) 에 대한 역원은 4죠.
더 나아가서, (ℤ/5ℤ,+ mod 5)는 abelian group 입니다.
일반적으로, any 정수 n에 대하여 (ℤ/nℤ,+ mod n)는 abelian group 입니다.
Caution
혹시 set 위에 주어진 equivalence relation이라는 개념이나 quotient 한다는 개념을 처음 들어보신다면 구글링을 추천 드립니다.. 반드시 찾아보세요. 찾아봐도 모르시겠으면 강의를 따로 올려드리죠.
그리고 주어진 예시 (ℤ/nℤ,+)는 나중에 가서 배울 quotient group 중에서 이해하기 가장 쉬운 예제입니다. 반드시 숙지하도록 하세요.
P.S. 다음 시간에 정의할 Cyclic group 과도 관련이 있습니다. 그때 가서 다시 보죠.
3. ({i,-1,-i,1},·)
복소수 i 는 다들 아실 거라고 생각합니다. 방정식 x^2+1=0 의 해 중에서 하나로 정해지는 수 입니다. (다시말해 i^2=-1)
i를 거듭제곱 해보세요. 그러면 다음과 같은 결과를 얻습니다:
i^2=i
i^2=i·i=-1
i^3=i·i^2=-i
i^4=i·i^3=1
따라서 {i,-1,-i,1} 같은 set을 생각할 수 있죠.
{i,-1,-i,1} 에 있는 원소들은 아무리 서로 곱해도 다시 {i,-1,-i,1}안에 들어갑니다.
따라서 곱 ·는 {i,-1,-i,1}위에서 binary operation(이항연산)이 됩니다.
결합법칙은 당연히 성립합니다.
1은 당연히 곱 ·에 대해 항등원이 되구요
각각의 원소의 역원은 한번 구해보세요.사실 역원을 구하는게 쉬운게, i^n 의 역원은 i^{4-n}이 겠죠. i^n ·i^{4-n}=i^4=1 이니깐요.
사실 ({i,-1,-i,1},·)는 (ℤ/4ℤ,+)와 대수적으로 완벽히 같습니다. Isomorphism 이라는 개념에 대해 조만간 포스팅 할건데 그 때 가서 다시 이 포스팅을 읽으시면 됩니다. (제가 글을 쓰면서 계속 복선을 깔고 있죠 ㅎㅎ)
글을 마치며
오늘 들어드린 예시는 정말 문제없이 이해할 정도로 쉽습니다. 이런식으로 기초공사를 1층부터 하면 더 어려운 수학도 전혀 문제 없습니다. 다함께 벽돌쌓기를 1층부터 해봅시다.
오늘은 이만 포스팅을 마치고, 다음시간에 더 다양한 예제와 함께 찾아뵙겠습니다. 명절 잘 보내세요.
Cheer Up!
quotient group 찾아봐야겠군요.
제 화웨이 폰에서는 문자들 잘 나옵니다. 감사합니다.
댓글 감사합니다. Cyclic group도 한번 찾아보시면 좋습니다.