'빚( - )에 빚( - )을 곱하는데 어떻게 재산( + )이 돼?'
음수의 곱셈을 처음 접한 뒤, 이 생각으로 한참 고민한 기억이 생각나네요...ㅠ.ㅠ
근데 이제보니 이렇게 해서 이해가 안 되는게 당연해요.
오죽하면 그 똑똑한 데카르트도 음수는 잘못된 수[1] 라고 거부했습니다.
(따라서 이번 글을 이해하고, 당시의 데카르트보다 똑똑해져 보아요)
그래서 저희는 빚에서 탈출해서 그림으로 이해해볼게요.
..., -4, 2, 1, -3, 0, -2, 3, ...
그럼 설명을 시작하면서, 위의 뒤죽박죽인 수를 가지런히 놓아봅시다.
우리는 0을 기준으로 오른쪽엔 하나씩 커지는 수를, 왼쪽에는 하나씩 작아지는 수를 놓을 수 있어요.
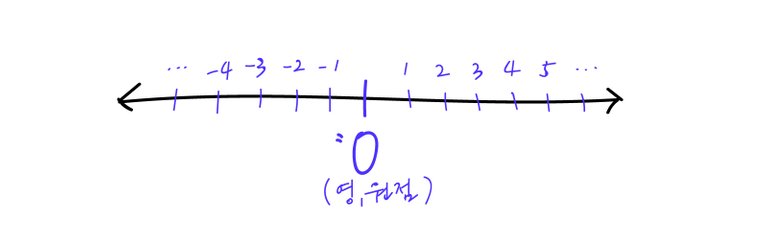
(여기서 0이 기준이 되는 이유는, '무'의 상태에서 하나씩 더해가는 수를 양의 음수(자연수), 하나씩 빼는 수를 음의 정수[2]라고 말할 수 있기 때문입니다. )
이때 0보다 큰 양수를 0(원점)을 기준으로 좌우로 뒤집으면, 0보다 작은 음수가 됨을 알 수 있어요.
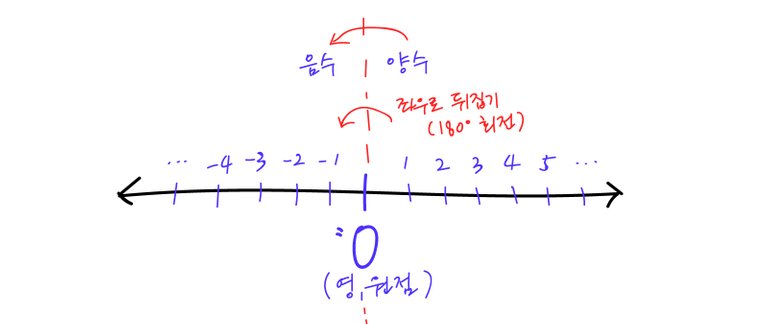
이렇게 '뒤집는' 느낌을 갖고 간단한 계산을 해봅시다.
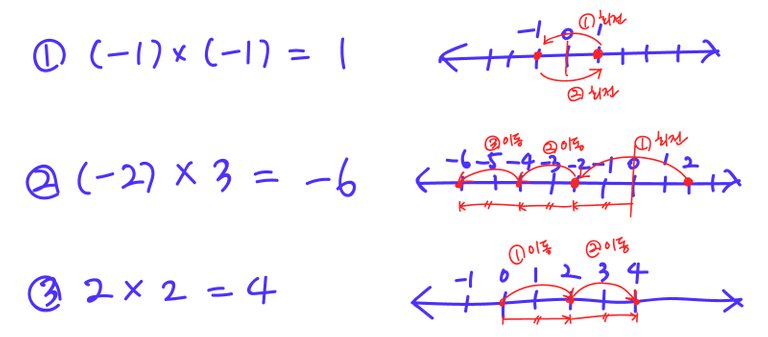
- (-1) 곱하기 (-1)
- 회전 : 1을 뒤집는다. 결과 : (-1)
- 회전 : (-1)을 다시 뒤집는다. 결과 : 1
- (-2) 곱하기 3
- 회전 : 2를 뒤집는다. 결과 : (-2)
- 이동 : (-2)만큼 1번 더 이동한다. 결과 : (-4)
- 이동 : (-2)만큼 1번 더 이동한다. 결과 : (-6)
- 2 곱하기 2
- 이동 : 2만큼 이동한다. 결과 : (2)
- 이동 : 2만큼 1번 더 이동한다. 결과 : (4)
여기까지 설명이 잘 되었나요?
이렇게 (음수) 곱하기 (음수)가 양수가 되는 이유를 수직선을 이용해 생각해 볼 수 있고, 혹은 대수적으로도 증명할 수 있습니다. 증명도 막상 해보면 어렵지 않으니 심심하시면 한번...! (힌트[3]는 붙임자료에)
여기 더해, 수를 회전시키는 개념은 1차원에 머무르던 실수를 2차원 복소수로 확장 할 수 있습니다.
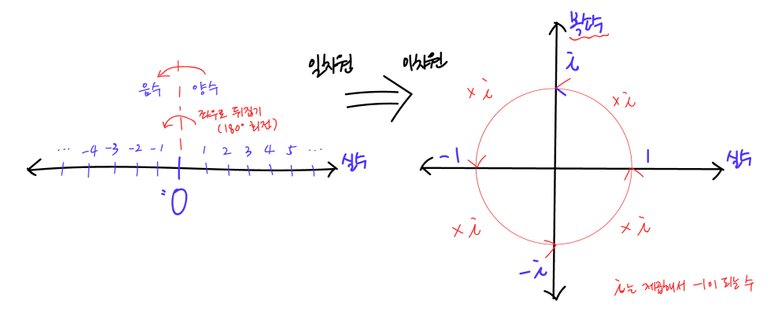
아래 동영상을 보시면 바로 이해가 되실거에요.
[4]: 더보기, '허수의 존재의 의미에 대해서', AngeloYeo,
'수학'을 주제로 글을 쓰면, 수학을 잘 한다고 생각하실 지 모르겠지만, 저는 성적표가 증명하는 수포자였어요. '수학은 좋아하는데 왜 이렇게 성적은 안 나왔을까' 하고 지금 생각하니 사소한 질문을 누릴 수 있는 여유가 없어서 그랬다는 변명도 좀 들 수 있을 것 같아요.
여튼, 당장 필요하진 않지만 안 하면 후회할 것으로 저에겐 '수학'이 있더라고요. 그래서 종종 책도 읽고 강의도 보고 있는데, (가끔) 같이 재밌어할 내용들이 발견되면 올려보려고 합니다. (의외로 저처럼 수학 공부를 다시 하고 싶어 하는 분들이 많더라고요)
시작하는 글은 <대수학 원론>에서 처음 이 내용을 읽고, 이해되지 않던게 이해되던 순간이 감격스러워서 꼭 이걸로 써보고 싶었어요. 소원 성취 했습니다ㅎㅎ 그럼 함께 글을 읽어주신 분들도 제가 느낀 감흥을 맛보길 바라며 마무리할게요!
(다 쓰고 보니 짜릿한 내용을 시들하게 전달한게 아닌지 걱정스런 마음도 듭니다만... 쓰다보면 점점 나아지겠죠..?)
붙임 자료
[1]: 더보기, '수학자도 거부한 수, 음수', 동아사이언스, http://mdl.dongascience.com/magazine/view/M200910N012
[2]: <레온하르트 오일러의 대수학 원론>, 레온하르트 오일러, 김성숙 외 옮김, 2015, p.18
[3]: 사각형의 넓이를 구한다고 생각하고, 사각형을 그려보면 쉽게 풀려요.
(해당 글에 첨부된 이미지는 대체 텍스트가 작성되어있습니다.)
보팅 버튼을 결국 찾아냈다...ㅎ
감사합니다 :P