안녕하세요. 암호화폐 관한 지적 대화를 위한 넓고 얇은 지식 시리즈를 연재하고 있는 흑두루미 개발자입니다.
(1) 해시 알고리즘
(2) 머클 트리 (본편)
(3) 비트 코인, POW의 해답인 Nonce? (예정)
(4) 암호 알고리즘, 공인 인증서 그리고 전자 서명 (예정)
(5) 왜 POW, 채굴에는 GPU를 사용하는가? (예정)
이번에 다룰 주제는 해시 알고리즘 응용의 결정체인 머클 트리(Merkle Tree)입니다.
최근 비탈릭 부테린과 댄 라리머의 논쟁에서 EOS가 이더리움보다 많은 거래(transaction)를 처리할 수 있는 이유 중 하나가 고의로 머클 트리 구현을 빠뜨린거라고 디스하기도 했었고, 무엇보다 “비트 코인, POW의 해답인 Nonce?” 편을 연재하기 전에 꼭 다루고 넘어가야 할 주제라고 생각하기 때문입니다.
머클 트리를 알아보기에 앞서 전산학에서 말하는 트리(tree)는 자료구조(Data Structure) 중 하나로 데이터를 배치하는 구성 요소가 뿌리(root), 줄기들이 교차하는 마디(node) 그리고 잎(leaf)으로 이루어져 있습니다. 아래의 나무 그림처럼 말이죠.
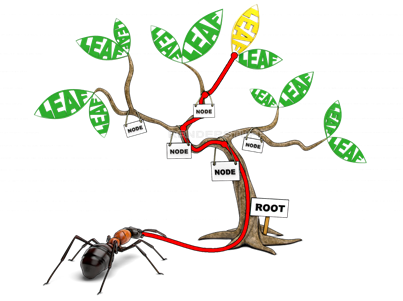
나무가 뿌리에서 시작하듯이 트리 구조도 항상 root에서 시작하며, root에서부터 시작한 줄기는 node를 만나서 여러 갈래의 줄기로 분화될 수 있고 그 줄기의 끝에는 또 다른 node가 있어서 다른 줄기들로 분화되거나 또는 줄기의 끝인 leaf일 수 있습니다.
크고 아름다운 저 개미가 저 많은 잎사귀 중에서 꿀발라놓은 노란색 잎를 찾으려면 빨간색 화살표를 따라가야만 하듯이 트리 구조에서 특정 데이터를 검색하는 경로는 항상 특정 노드(node)를 거쳐야 합니다.
사실 트리 구조는 우리 일상에서 아주 밀접한 “Windows 탐색기”에서도 많이 쓰이는 방식입니다.
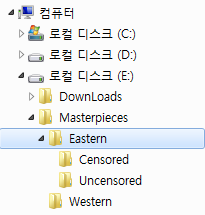
로컬 디스크(E:)를 뿌리(root)라고 가정하면, 각각의 폴더들은 하나 이상의 폴더 또는 파일을 포함할 수 있으므로 노드로 볼 수 있지만, 파일은 파일이나 폴더를 포함할 수 없으므로 트리 구조의 가장 말단(terminal)인 leaf에 해당합니다.
계층(hierarchy) 관계로 보자면, 로컬 디스크(E:)의 자식 노드는 Downloads와 Masterpieces 폴더이고, Masterpieces 폴더는 Eastern과 Western 폴더의 부모 노드이며, Eastern 폴더는 Censored와 Uncensored 폴더를 자식 노드로 두고 있습니다.
그런데 말입니다. 이렇게 트리에 자료를 보관하는 이유는 무엇일까요?
트리는 계층 구조를 가지기 때문에 노드 단위로 자료를 관리할 수 있고 검색 시간도 단축할 수 있습니다.
저 탐색기의 소유자를 존경하는 누군가가 어느날 갑자기 저 컴퓨터를 5초 뒤에 살펴보고 싶다고 통보해왔습니다. Censored, Uncensored 그리고 Western 폴더에 매우 프라이빗한 파일들을 보관했다고 가정한다면…!?
그냥 5초 뒤에 누군가의 존경을 잃어버리던가 혹은 이러한 자료들을 모두 포함하는 부모 노드인 Masterpieces 폴더를 선택하여 Shift+Del 키를 누르는 선택지가 있을겁니다.
후자의 결단이 떠오르셨다면 여러분은 이미 트리 구조에서 폴더(node)와 파일(leaf)이 가진 부모(parent)-자식(child)간의 계층 관계를 본질적으로 이해하고 계신겁니다.
검열이 지난 얼마 후에 저 탐색기의 소유자는 프라이빗한 자료들을 다시 수집하기 시작합니다.
정적인 아름다움이 동적인 것만큼 아름다울 수 있다는 진리를 깨닫게 되어 이전에 별도로 관리하고 있던 Photos라는 폴더를 Masterpieces 폴더 안에 옮기게 되었습니다.
그리고 동적인 자료들로 구성된 Eastern와 Western 폴더들을 Movies라는 폴더를 만들어 그 안에 옮겼습니다.
폴더(node)들의 배치는 이전보다 복잡해진 듯 하지만 원하는 자료를 찾는데 걸리는 시간은 어떨까요?
동양인 선남선녀가 같이 건강하게 운동하는 동영상을 찾아보려 합니다. 또는 선남선녀들의 여름을 느낄 수 있는 순간의 미를 찾으려고 합니다. 어느 폴더에 원하는 파일이 있는지 바로 떠올릴 수 있지 않습니까? 트리 구조 만세입니다.
만약 하나의 폴더에 모든 파일들을 분류없이 넣어두었다면, 이름과 확장자를 모두 살펴본 후에야 찾을 수 있을테니까요.
다시 주제인 머클 트리(Merkle Tree)로 돌아가기 전에 하나만 더, 이진 트리(Binary Tree)라는 것을 살펴보겠습니다.
이진 트리에서 root와 node는 0과 1, 단 2개의 기호를 쓰는 이진법(binary)처럼 자식을 2개까지만 가질 수 있습니다.
이러한 제한을 하는 이유는 어떠한 기준을 적용하여 검색 시간을 단축하기 위해서입니다.
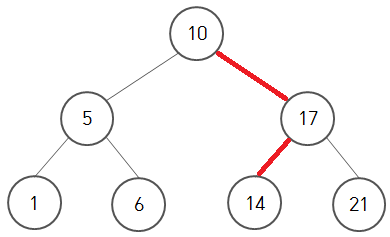
14라는 값을 검색하려면 root(10)에서 시작하여
- 10보다 14가 크기 때문에 오른쪽 node인 17을 선택합니다.
- 17보다 14가 작기 때문에 왼쪽 node인 14를 선택합니다.
- 선택한 14는 검색하려는 14와 같은 값이므로 검색을 완료합니다.
위의 이진 트리는 검색 시간을 단축하기 위하여 node의 값들을 크기 순으로 미리 수평 정렬한 이진 탐색 트리(Binary Search Tree)이므로, 값이 1, 5, 6, 21인 node들을 검색에서 배제하여 수행 시간을 단축할 수 있습니다.
잠깐 전문 지식하고 가실게요. (수학 울렁증을 가진 분들은 건너 뛰실게요.)
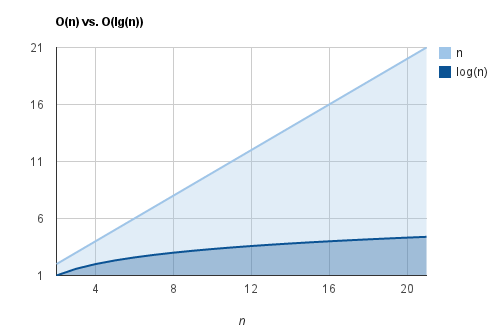
전산학에서 문제를 해결하는데 걸리는 시간과 함수(공식) 사이의 관계를 시간 복잡도 O(n)이라고 표현하고 이 시간 복잡도를 감소시키는 작업을 알고리즘의 최적화라고 정의할 수 있습니다.
앞선 그림에서 살펴본 이진 탐색 트리의 7개 node들을 다음과 같이 무작위로 일렬 배치해보겠습니다.
{ 1, 6, 5, 10, 17, 21, 14 }14를 검색하려면 처음 숫자인 1부터 하나 하나 숫자들과 반복 비교하여 마지막 숫자인 14까지 모두 7번을 반복해야 작업을 완료할 수 있습니다.
여기서 node의 개수가 더 증가한다면, 최악의 경우를 가정한 시간 복잡도 O(n) 또한 그에 비례하여 증가하므로 연한 하늘색의 선형 그래프처럼 표현할 수 있습니다.진한 하늘색의 그래프는 무작위 일렬 배치한 node들을 검색하는 것과 달리, 이진 탐색 트리의 검색은 node의 개수가 증가한다고 해도 시간 복잡도는 그에 비례하여 증가하지 않는다는 의미입니다.
앞선 그림의 이진 탐색 트리의 node 개수는 7개지만 root부터 가장 하위 node까지의 개수인 트리의 길이는 3입니다.
log27 = 2.807… ≈ 3, 즉 최악의 경우를 가정해도 7개의 node 중에서 3개의 node만 탐색하면 검색을 완료할 수 있습니다.참고로 이진 탐색 트리의 검색에서 시간 복잡도는 O(log2N) 이며, 이러한 검색 효율은 데이터베이스에서 검색을 최적화하는 인덱싱의 기본 원리이기도 합니다.
머클 트리는 가장 말단을 제외한 (non-leaf) 노드들이 자식 노드의 정보를 해시한 값으로 이루어진 이진 트리이며, 발명자 랄프 머클(Ralph Merkle)이 1979년에 특허 출원했다고 합니다.
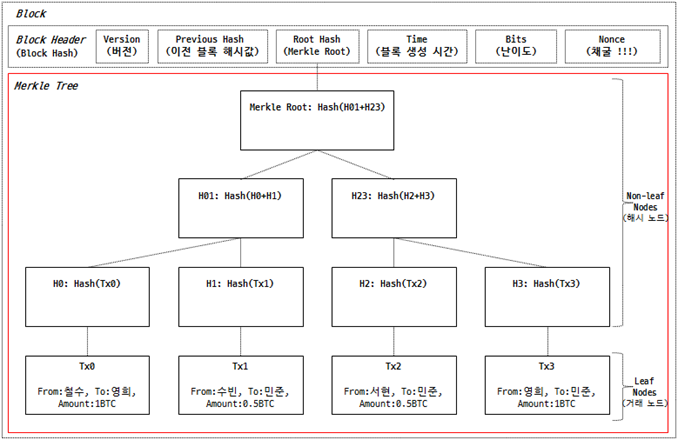
비트 코인에서 하나의 블록(block)은 헤더(header)와 거래(transaction) 정보들이 담겨져 있으며, 블록의 헤더(header)는 아래와 같이 구성되어 있습니다.
- Version: 블록의 버전
- Previous Hash: 현재 블록과 이미 이전에 생성된 블록 사이를 연결하기 위하여 이전 블록의 블록 해시(Block Hash)를 가리키는 값
- Merkle Root: 머클 트리의 루트 값
- Time: 블록 생성 시간
- Bits: 채굴(Proof Of Work: 작업 증명) 난이도
- Nonce: 채굴 난이도에서 설정한 값보다 작은 블록 해시 값을 구하기 위하여 사용되는 숫자 카운터, 채굴의 핵심 !!!
블록 헤더는 이번편에서 집중적으로 다루는 머클 트리의 루트 노드 값을 포함하기 때문에 간단하게 언급하였습니다만 자세한 설명은 다음 강좌인 “비트 코인, POW의 해답인 Nonce?” 편에서 꼼꼼하게 다루도록 하고 넘어가겠습니다.
그림에서 빨간색 박스로 둘러싼 부분이 바로 이 머클 트리입니다.
“머클 트리는 가장 말단을 제외한 (non-leaf) 노드들이 자식 노드의 데이터를 해시한 값으로 이루어진 이진 트리”라고 했습니다. 여기서 “가장 말단을 제외한 (non-leaf) 노드들”을 강조하는 이유는 가장 말단 노드(leaf)는 거래 내용을 가지고 있고, 말단을 제외한 나머지 모든 노드들은 각각의 자식 노드의 정보를 해시한 값을 가지고 있기 때문이며, 모든 부모 노드들은 자식 노드를 최대 2개까지만 가질 수 있는 이진 트리 형식입니다.
복잡해 보이긴 합니다만 백문이 불여일타라고 했습니다. 지금부터 나오는 내용들을 직접 따라해 보시면 이해에 도움이 될겁니다.
앞선 그림에서 거래(Tx: Transaction) 내용 중 하나인 Tx0은 철수가 영희에게 1비트 코인을 전송했다는 의미로 “From:철수, To:영희, Amount:1BTC” 라고 표현했습니다.
실제로 비트 코인에서의 거래 내용은 스크립트 형식으로 이루어져 있으며 자세한 내용은 https://en.bitcoin.it/wiki/Script 을 참고하세요.
http://www.whatsmyip.org/hash-generator/ 사이트로 가서 Input String란에 “From:철수, To:영희, Amount:1BTC” 를 입력하고 Calculate Hashes 버튼을 클릭하면 아래처럼 해시 값들이 출력됩니다. 이왕이면 비트 코인에서 사용되는 sha256 해시 알고리즘으로 진행해보겠습니다.
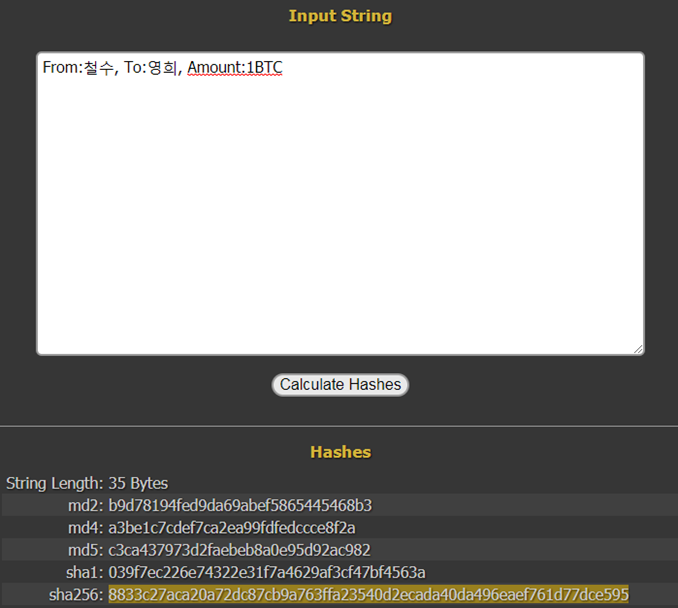
이를 수식처럼 그럴듯하게 표현해보겠습니다.
Hash(Tx0): sha256(“From:철수, To:영희, Amount:1BTC”) = 8833c27aca20a72dc87cb9a763ffa23540d2ecada40da496eaef761d77dce595
마찬가지로 Tx1, Tx2, Tx3도 각각 해시 값을 구해보면 아래와 같은 결과가 나옵니다.
Hash(Tx1): sha256(“From:수빈, To:민준, Amount:0.5BTC”) = 8637ac553a5ab922b18058d623b5128e1f9d39f3bccafb31afd0250dabcbc60d
Hash(Tx2): sha256(“From:서현, To:민준, Amount:0.5BTC”) = 956879a5c44cc228250e49e941248150486dfccbdee553cc52aca2ca3780207d
Hash(Tx3): sha256(“From:영희, To:민준, Amount:1BTC”) = f25327ff5ab8963d1f1ee2a6b6c7f8380ceb37ff7d783a4c0fcc62ac4f320a45
이렇게 거래 노드들(Tx0, Tx1, Tx2, Tx3)의 내용을 해시한 값들은 아래 그림처럼 그 부모 노드들(H0, H1, H2, H3)에 표시한 빨간색 이름표가 됩니다. 짜잔~~~
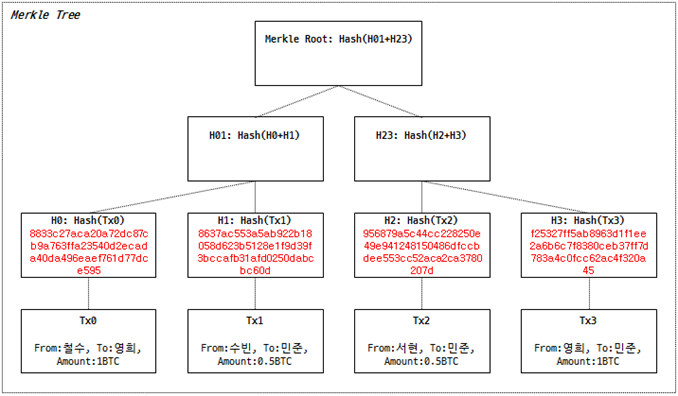
이제 H01 노드와 H23 노드에 들어갈 해시 값을 구해보겠습니다.
H01 노드의 자식 노드는 H0 노드와 H1 노드이므로, H0:“8833c27aca20a72dc87cb9a763ffa23540d2ecada40da496eaef761d77dce595”과 H1:“8637ac553a5ab922b18058d623b5128e1f9d39f3bccafb31afd0250dabcbc60d”을 합쳐서 해시 값을 구하면
Hash(H0+H1): sha256(“8833c27aca20a72dc87cb9a763ffa23540d2ecada40da496eaef761d77dce5958637ac553a5ab922b18058d623b5128e1f9d39f3bccafb31afd0250dabcbc60d”) = cf63c2a4c35648cc6484ffa0980926282959363c8ddf1eda7936efbe73b98d2b
마찬가지로 H23 노드의 자식 노드는 H2 노드와 H3 노드이므로
Hash(H2+H3):
sha(“956879a5c44cc228250e49e941248150486dfccbdee553cc52aca2ca3780207df25327ff5ab8963d1f1ee2a6b6c7f8380ceb37ff7d783a4c0fcc62ac4f320a45”)
= b0e3623c02a5b9087d08e676f1bcbb63ef8f24337c097c21d9e9e8f86e912ad4
이 해시 값들을 H01 노드와 H23 노드에 빨간색으로 표시하도록 하겠습니다.
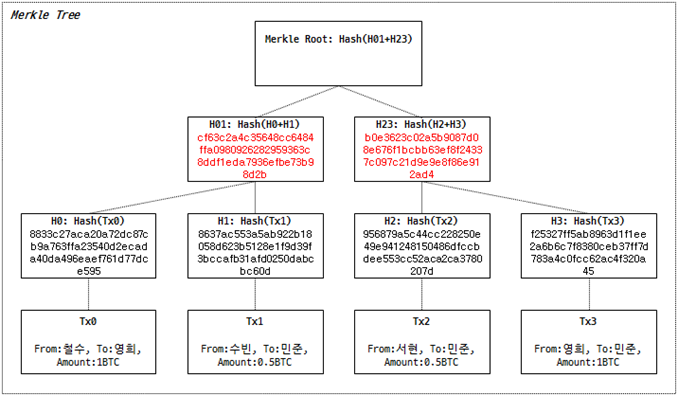
이제 머클 루트 노드만 남았습니다. 루트 노드의 자식 노드는 H01 노드와 H23 노드이므로
Hash(H01+H23): sha(“cf63c2a4c35648cc6484ffa0980926282959363c8ddf1eda7936efbe73b98d2bb0e3623c02a5b9087d08e676f1bcbb63ef8f24337c097c21d9e9e8f86e912ad4”) = 5832658fb927c9f62064d833f0e14a8ff34fa5858154a81b51ba92ecef752efd
이 해시 값을 머클 루트 노드에 빨간색으로 표시하도록 하겠습니다.
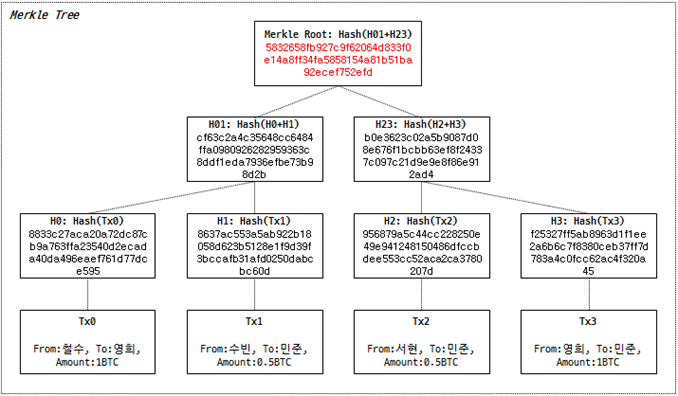
수고하셨습니다. 드디어 머클 트리를 완성했습니다.
지난 강좌인 “(1) 해시 알고리즘” 편에서 언급했듯이 해시 알고리즘은 입력 값의 길이에 상관 없이 출력 값의 길이는 항상 일정합니다. 따라서 가장 말단인 거래 노드들을 제외한 모든 노드들이 가지는 해시 값 길이는 64문자(16진수)로 모두 같습니다.
지금까지 하나의 블록 안에 포함된 거래들의 유효성을 해시 알고리즘을 사용하여 노드 별로 단계적으로 검증하는 구조인 머클 트리를 알아보았습니다.
다음 편 예고
거래 장부들에 따르면, 철수는 영희에게 소중한 1비트 코인을 선물로 전송했고, 수빈과 서현은 민준에게 0.5비트씩 모두 1비트 코인을 전송했습니다. 그리고 영희는 철수에게 받은 1비트 코인을 민준에게 선물로 전송했습니다.
이 사실을 알고 분노한 우리의 흑우 철수는 능력자 민준에게 복수를 다짐하며 거래 장부 Tx0을 “From: 민준, To: 철수, Amount: 2BTC”로 조작하여 민준이 받은 2비트 코인을 모두 자신에게 전송할 계획을 세웠습니다.
이번 편에서 머클 트리를 학습한 철수는 Tx0 거래 노드에 연결된 모든 노드들(H0, H01, 머클 루트)의 해시 값을 모두 조작하려고 할 것입니다.
철수의 복수는 이루어질 것인지 아니면 다음에 연재할 “비트 코인, POW의 해답인 Nonce?” 편에서 블록 체인의 진실을 마주하고 목이 돌아갈까요? To be continued...
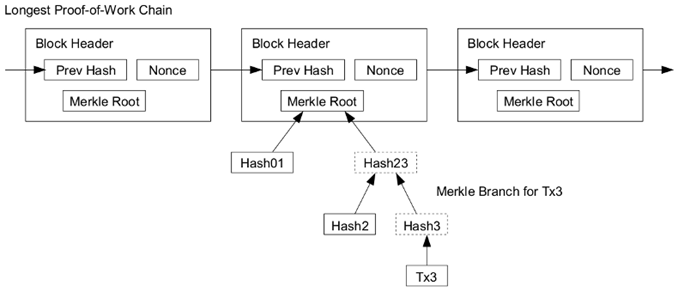
아마도 철수는 이런 진실을 만나겠죠...? 출처: https://bitcoin.org/bitcoin.pdf
다음 편에서는 이러한 블록들을 연결한 블록 체인이 어떻게 서로를 검증하는지, 왜 채굴(Proof Of Work)이 블록 체인의 안전을 보장할 수 있는지에 관하여 써보려고 합니다.
본글의 저작권은 저자에게 있으며, 저자의 허가없는 사용 및 도용을 금지하니 양해 바랍니다.
Congratulations @loveiori! You received a personal award!
Click here to view your Board
Congratulations @loveiori! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!