
[3]
팔로워 수에 숨겨진 수학 - Friendship 패러독스
1. 스팀잇의 수학적 모델링
스팀잇은 팔로우와 팔로워가 구별된다.
A가 B를 팔로우하면 다음과 같이 A에서 시작하여 B로 가는 화살표로 나타내자.

마찬가지로 B가 A를 팔로우하면, 다음과 같이 B에서 시작하여 A로 가는 화살표를 덧댄다.

이렇게 스팀잇의 모든 팔로우, 팔로워 관계를 방향성 그래프 로 나타낼 수 있다. 예를 들어서

의 경우 A,B 그리고 D,E 는 서로를 맞팔 중이고 G는 그 어떤 사람과도 교류를 하고 있지 않은 것이다. 물론 자기가 자기를 팔로우 할 수 는 없으므로 loop 은 존재하지 않는다.
2. 팔로워 팔로우 구분해보자!
일단 A, B, C, ... 는 너무 불편하므로 숫자 1,2,... 을 사용하겠다. SNS 상에 

- 숫자
에
가
를 팔로우 했을 경우, 즉

경우 1을 부여하고, 그렇지 않은 경우 0을 부여한다. 이들을 모두 모아서 
)
가 팔로우 중인 사람들은 총 몇 명 일까?
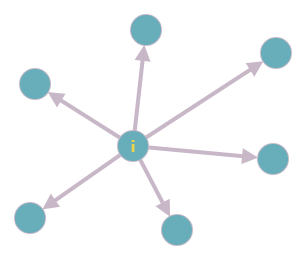
이는 다시 말해서 

로 놓는다.
- 마찬가지로
의 팔로워는 총 몇 명 일까?
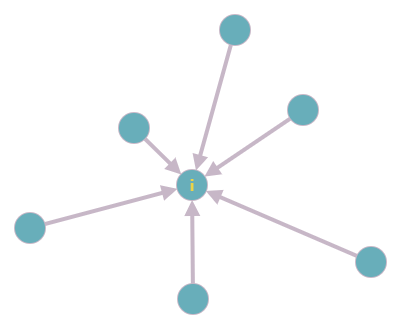
이는 다시 말해서 


로 놓는다.
3. 스팀잇에서 나는 뭘까?
대부분의 사람들이 팔로워 수에 굉장히 민감하다. 많으면 많을 수록 스팀잇에서 영향력이 높은 사람이라 간주되기 때문이다. 열심히 팔로워를 늘리고, 동시에 다른 사람들을 팔로우 하다 보면 다음과 같은 사실에 좌절할 때가 있다.
내가 팔로우 한 사람들은 평균적으로 내 팔로워 수 보다 많은 팔로워를 보유하고 있다.
물론 고래나 관리자, 운영자 등 특수 계정은 해당되지 않고 모든 사람들이 이러한 사실을 만족하지는 않는다. 그러나 많은 사람들이 이러한 사실에 좌절하곤 한다. 또한 역으로 나를 팔로우 한 사람의 계정을 클릭해 들어가보면
나를 팔로우 한 사람들은 평균적으로 나보다 더 많은 사람들을 팔로우 하고 있다.
라는 신기한 사실에 맞닥뜨린다. 그런데, 수학적으로 생각해보면 이러한 특징들을 만족하는 사람들은 스팀잇에 생각보다 꽤 많이 존재한다. 이제부터 왜 그런지 알아보자.
4. 약간의 수학...
먼저 다음과 같은 암울한 상황에 대해 알아보자.
내가 팔로우 한 사람들은 평균적으로 내 팔로워 수 보다 많은 팔로워를 보유하고 있다.
이 것을 수학적으로 생각해 보면 다음을 증명하는 것과 같다.
 개개인 마다 팔로우한 사람들의 팔로워 수의 평균
개개인 마다 팔로우한 사람들의 팔로워 수의 평균 SNS 상 각 사람들의 팔로워 수의 평균은 우리가 section 2에서 정의한 변수 

이다. 이제 남은 각 사람들의 팔로워의 팔로워 수의 평균을 구해보자. 





이다. 전체 

가 된다. 이제 우리가 증명하고자 하는 것은
^2&space;\leq&space;n&space;\sum_{i}\sum_{j}a_{ij}d_{j}^{\text{in}})
로 단순화 된다. 더욱이
^2)
이므로 코시-슈바르츠 부등식에 의해 우리가 원하던 부등식
^2&space;\leq&space;\left(&space;\sum_{i}&space;1^2&space;\right)&space;\sum_{j}&space;(d_{j}^{\text{in}})^2&space;=&space;n&space;\sum_{j}&space;(d_{j}^{\text{in}})^2)
이 나온다. 따라서
평균적으로 내가 팔로우 한 사람들의 팔로워 수 평균은 내 팔로워 수 보다 크거나 같다.
다음으로 신기한 상황을 분석해보자.
나를 팔로우 한 사람들은 평균적으로 나보다 더 많은 사람들을 팔로우 하고 있다.
누가 날 팔로우해서 가봤더니만 봇 ;(. 사실 이 경우는 위의 경우와 똑같은 데, 단지 


이 성립해야 한다. 또한
^2&space;&=&space;\sum_{i}&space;d_{i}^{\text{in}}&space;d_{i}^{\text{in}}&space;\\&space;&=&space;\sum_{i}&space;d_{i}^{\text{in}}&space;\left(&space;\sum_{j}&space;a_{ji}&space;\right&space;)&space;\\&space;&=&space;\sum_{j}&space;a_{ji}&space;\left(&space;\sum_{i}&space;d_{i}^{\text{in}}&space;\right)&space;\\&space;&=&space;\sum_{j}&space;a_{ji}&space;\left(&space;\sum_{i}&space;d_{i}^{\text{out}}&space;\right)&space;\\&space;&=&space;\sum_{i}&space;(d_{i}^{\text{out}})^2&space;\end{align*})
따라서 암울한 상황의 식에 대입하면
^2&space;\leq&space;n&space;\sum_{i}&space;(d_{i}^{\text{out}})^2)
끝!
평균적으로 나를 팔로우 한 사람들의 팔로우 수 평균은 내 팔로우 수 보다 크거나 같다.
5. 결론
평균적으로 난 내가 팔로우한 사람들보다 팔로워 수가 적은 상황에 놓일 가능성이 높다. 굳이 스팀잇이 아니라도, 어느 SNS에서나 성립한다. 다만 스팀잇의 경우 뉴비는 이러한 상황에 놓일 가능성이 타 SNS보다 월등히 높다.
그렇다면 모든 사람이 암울하고 좌절하지 않게 할 수 는 없을까? 부등식의 등호가 성립할 조건을 살펴보면, (코시 슈바르츠 등호 성립조건 참조)

즉 모든 사람이 똑같은 팔로워 수를 보유하고 있을 때에만 가능한 얘기임을 알 수 있다. 상식적으로 SNS 상 모든 사람이 똑같은 팔로워 수를 보유하고 있는 것은 말도 안되므로 불가능한 소리!
- 자기가 둘 다에 해당하는지, 혹은 한 가지 상황에만 해당하는지, 아니면 해당사항이 없는지 체크해보는 것도 재밌을 것이다.
6. 출처/ 인용
[1] https://arxiv.org/pdf/1807.01496.pdf
[2] 그래프의 경우, http://graphonline.ru/en/ 에서 제공하는 툴을 사용하였습니다.
[3] https://steemit.com/steemit/@brandonfrye/how-to-gain-steemit-followers-and-upvotes-the-legit-way (사진 출처)
수식은 못 알아듣겠지만 접근하신 방법이 재미있네요.
이런 생각을 하실 수 있다는게 남다르신 것 같습니다.
읽어주셔서 감사합니다!
@_@;; 저는 그저 다른행성에서 쓰는 언어로 보이네요 흑흑
재밌는 수학적 접근이네요.
이 가설이 증명될려면 팔로우와 팔로워을 하는 이유에 대한변수가 명확하게 정의되어 있어야 하기 때문에 사실 증명은 좀 어렵다고 생각되네요. 그리고 post의 질, 활동지수, 스파 등 이외에도 더 많은 다양한 변수들이 팔로우와 팔로워에 미치는 변수로 영향을 주게 되지요.
전제 조건인 되는 여러 상황들의 변수가 너무 많기 때문에 어떤 하나의 조건으로 일반화하는 건 성급한 결론을 낳게 되는 것 같아요.
재밌게 잘 읽었습니다^^
역시 흥미로운 소재는 어려운 이야기도 재미있게 읽게 되는것 같아요^^
이오스 계정이 없다면 마나마인에서 만든 계정생성툴을 사용해보는건 어떨까요?
https://steemit.com/kr/@virus707/2uepul