최근에 어떤 분이 재미있는 문제를 소개해주셔서 그 문제에 대해 글을 작성할까 한다. "모든 자연수의 분할수의 역수의 합이 수렴함"을 증명하는 문제였는데 그 당시에는 조금 어려운 방법으로 풀었었지만 운 좋게도 우연히 더 쉽고 아름다운 풀이를 알게 되었다.

먼저 '분할수'란 무엇일까? 쉽게 설명하면, n의 분할수 p(n)은 n을 자연수의 합으로 나타내는 방법의 수를 말한다. 자연수 6의 경우를 보자. 6을 자연수의 합으로 나타내는 방법의 수는 몇 가지나 될까?
6 (이렇게 쓰는 경우도 한 가지로 본다.)
5+1 (주의 : 1+5나 5+1 은 같은 경우로 본다.)
4+2
4+1+1
3+3
3+2+1
3+1+1+1
2+2+2
2+2+1+1
2+1+1+1+1
1+1+1+1+1+1
총 11가지다. 따라서 6의 분할수, p(6)은 11과 같다.
사실 n의 값이 커질 때 p(n)은 대략
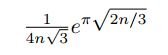
에 근접한다는 사실이 알려져 있지만 문제에서 그걸 이용할 것을 의도하지는 않았을 것으로 보인다.
문제에서 요구한 급수의 수렴성을 보이기 위해 자연수 n을 세 개의 자연수의 합으로 나타내는 방법의 수를
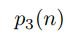
이라 하자. n이 3 이상이면 이 값이 1 이상 p(n) 이하의 정수라는 것은 당연하다. 이제
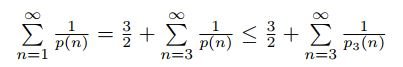
이므로 우리는 급수
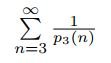
가 수렴함을 보이면 된다.
여기서 놀랍게도 우리는
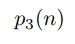
의 일반항을 구할 수 있는데 결론부터 말하자면 우리가 쉽게 접하는 등차수열의 일반항
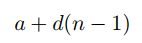
이나 피보나치 수열의 일반항
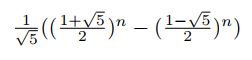
등등과는 조금 다른 모습으로 주어진다.
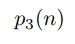
의 일반항은
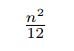
에 가장 가까운 정수다.
따라서 급수
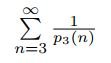
의 수렴성은 바젤 문제로도 유명한 다음 급수
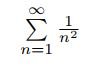
와의 비교판정법으로 쉽게 증명된다.
글이 길어질 것 같아
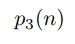
의 일반항을 구하는 방법은 다음 글에서 다뤄보도록 한다.
It looks like it has to do with partitions. Ramanujan did some amazing work in this field. Looking forward to the English version.
You're right. In this post, I introduced a problem that requires to prove the infinite sum of the reciprocals of the partitions of the positive integers converges.
The English version of this post will be uploaded soon.
먼저 하디 라마누잔 공식이 눈에 띄는군요 ㅎㅎ
저에게는 이 partition number 가 q pochhammer function 즉 modular properties 계산으로 친숙하긴 한데, p_3(n) 3개로 쪼개는 경우는 처음 봤네요 ㅎㅎ 앞으로의 전개가 많이 기대되네요 ~~ ㅎㅎ
다음 글.. 작성해야 하는데 수식 입력이 너무 성가셔서 자꾸 미뤄지네요 ㅋㅋ