This is just the English version of my previous post : [수열과 생성함수 01]
Recently, someone introduced me an interesting problem, so I'm just writing about that. The problem says, "Prove that the infinite sum of the reciprocals of the function values of the partition function for the positive integers converges," and I solved it using a quite complicated way at that time. However, luckily, I got to know an easier and more beautiful solution for that problem by some chance.

First, what does the term 'partition function' means? The function value of the partition function for a positive integer n is just the number of ways of expressing n as a sum of positive integers. Take 6 for example. How many ways are there to express 6 as a sum of positive integers?
6 (We also count this as one way.)
5+1 (Caution : We think 1+5 and 5+1 are the same.)
4+2
4+1+1
3+3
3+2+1
3+1+1+1
2+2+2
2+2+1+1
2+1+1+1+1
1+1+1+1+1+1
Total 11 ways. Therefore, the function value p(6) of the partition function for 6 is equal to 11.
In fact, it is known that p(n) is asymptotically equal to
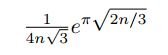
as n grows, however, the problem doesn't seem to be the asking us to use that fact.
To show the given infinite sum converges, let
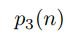
denote the number of ways of expressing n as a sum of three positive integers. It is clear that the output of this function is a positive integer not greater than p(n) if n is not less than 3. Since
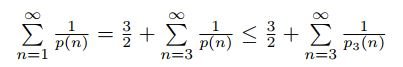
holds, we only need to show that the series
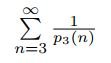
converges.
Surprisingly, we can find the general formula for computing
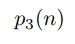
, and this formula looks quite different from the general formulas we know, the general formula
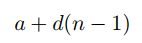
for an arithmetic progression or the general formula
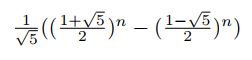
for the Fibonacci sequence, for instance. The value
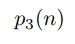
is equal to the nearest integer to
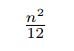
. So, we can prove the convergence of the series
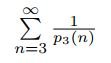
by using the direct comparison test with the well-known series
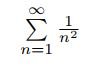
which appears in the Basel problem.
To avoid this post to be too long, I'll just stop here and I'll deal with the way to find the general formula for
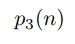
in my next post.
Any mathematical comments and English corrections are welcome :)
A clever way to prove it, impressive work!