Hello everyone!

If you've been following me you'd already know that I'm interested in Cellular Automata and its applications. This time I've simply visualised what would happen to play god in this cellular automata universe and added my spices to it. Usually this is done by setting the initial cells/initial grid and let it run and see what it would look like after "x" number of evolutions. In this application you can intervene to the world, kill and spawn cells while they are evolving...
If you don't want to see any programming stuff head to Results section to see what my world evolves in to. I added gifs if you are no programmer.

Introduction

Cellular automatons are mathematical models which many components of the system acts as one depending on other components to produce a complicated patterns of behaviour. Cellular Automaton consists of a grid of cells each, in finite number of states. At initial state t=0 states are defined for the cells. For each cell a set of a neighbourhood is defined relative to the chosen cell. A new generation is created per a fixed rule that determines the next state of the cell regarding their neighbours. Rules usually do not change over generation although some exceptions are known such as asynchronous cellular automaton. Cellular Automata has a history starting from the 1940s with Stanislaw Ulam and John van Neumann[1]. John van Neumann tried to develop an abstract model of self-production in biology as a 3D model. Later Stanislaw Ulam developed a version of cellular automata in 2D and implemented it on analogue circuitry. In 1960s Stanislaw Ulam and others used computers to simulate 2D cellular automata. Later in the 1970s inspired by the “simulation games” of Ulam and others, motivated by the questions in mathematical logic, John Conway invented Conway’s Game of Life, two-dimensional cellular automata with its own set of rules. John Conway did exhaustive research to find repetitive patterns and behaviours in cellular automata. The game is designed around the following rules [2] :

Any live cell with fewer than two live neighbours dies, as if caused by underpopulation. Shown on first, third and fourth example on Figure 1.1.
Any live cell with more than three live neighbours dies, as if by overcrowding. See Figure 1.1 example 2.
Figure 1.1:Conway’s Game of Life Death Scenario[2]
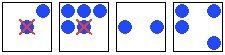
Any live cell with two or three live neighbours lives on to the next generation. Shown on Figure 1.2
Figure 1.2: Conway’s Game of Life Survival Scenario[2]
Any dead cell with exactly three live neighbours becomes a live cell. See Figure 1.3

Figure 1.3: Conway’s Game of Life Birth Scenario [2]*

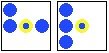
Cells can be evaluated by using the either of the following neighbourhoods for radius=1 shown in Figure 1.4. Black cells shows the evaluated cells for counting the neighbours.
Figure 1.4 Von Neumann Neighbourhood (Left) Moore Neighbourhood (Right)*

This project considers using Moore Neighbourhood with rules defined by John Conway’s Game of Life.
This project aims to visualise the complex behaviour of Conway’s Game of Life using CUDA and OpenGL with a suitable Nvidia graphics card. The project will focus on the visualisation part rather than the optimization of the cellular automata on GPU’s. Focusing on visualisation will help understanding the underlying chaotic behaviour and also helps generate complex states of the cells using colours. This also brings the advantage of executing processes within the GPU memory and outputting straight from the GPU memory.
Two dimensional cellular automatons are often used to simulate fluid and gas dynamic systems but also has other uses such as crystal growth and reaction-diffusion systems.

CUDA – OpenGL Interoperability

CUDA was created to take advantage of the parallel processing power of the graphics processor units (GPU). Cellular Automaton structure is made of a grid of cells where they can be evaluated in parallel to obtain speedups compared to serial evaluation of the cells. CUDA will be used to calculate the neighbours of a cell then the resulting cells will be drawn on the screen using the Open GL library. Open Graphics Library (Open GL) is a cross-language API (Application Programming Interface) for rendering 2D or 3D vector graphics using the graphics processor unit. To interact with the OpenGL window, “freeglut” library will be used to handle keyboard presses and mouse movements.
CUDA uses familiar C memory management techniques such as cudaMemset, cudaAlloc. Open GL uses a different concept called “buffer objects”. To use the CUDA memory within the OpenGL context, Open GL buffer objects has to be mapped to the memory that resides in the CUDA context before it can be shown on the screen. In this project pixels are generated within the CUDA context and needs to be mapped to the texture buffer in OpenGL. Once the memory mapping to the OpenGL is complete it can be displayed within the OpenGL window. Then the OpenGL context can be edited using the CUDA context since both contexts reside in GPU and eliminates the need to return the data to the CPU. Figure 2.1 shows generalised relation between CPU, CUDA context and OpenGL context. Then Figure 2.2 explains how visualisation within the GPU memory happens with the use of OpenGL interoperability.

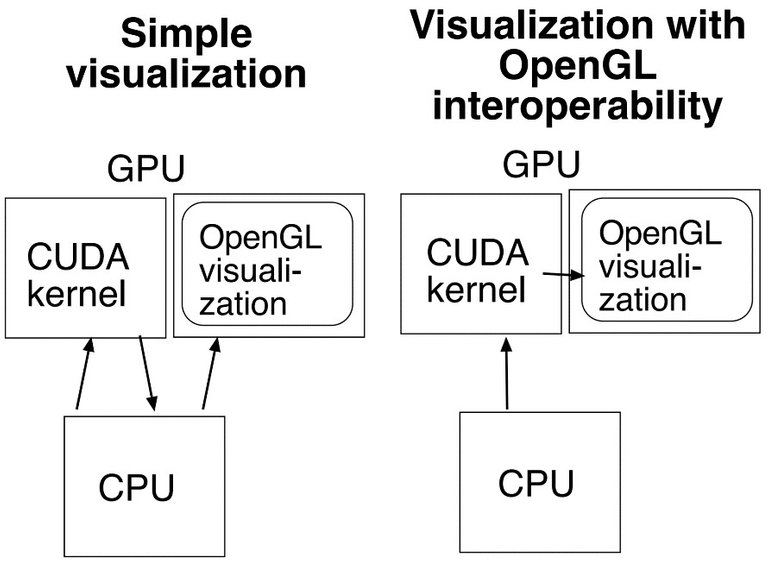
Figure 2.1: Visualisation without interoperability (left) and Visualisation with interoperability (right)[3]

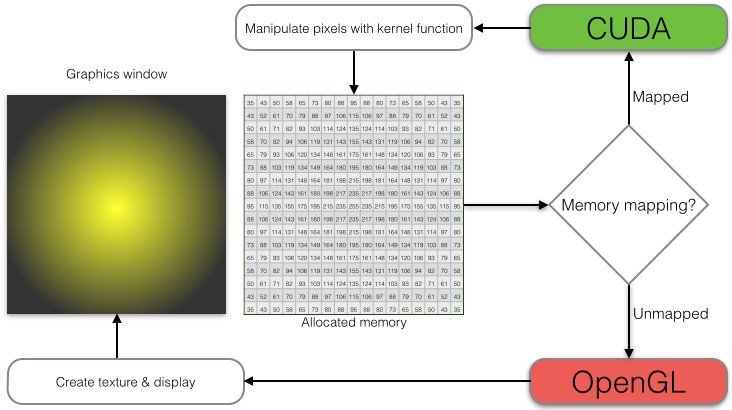
Figure 2.2: CUDA & OpenGL Interoperability [3]

Proposed Solution

Conway’s Game of Life is a well-known cellular automata that simulates an artificial life consisting a grid of cells which they can have only two states “dead or alive”. It must be noted that the only human interaction with this world is the initial state of the cells. The project will aim to give more states to each cell and represent those different states with various colours so that the world becomes more complex. This will be then paired with “freeglut” (Graphics Library Utility Toolkit) to allow human interactions with the world on runtime. This will allow the user to zoom in, move around the world (perspective change) and manipulate the cells on run time. The use of CUDA kernels will come in handy when evaluating the neighbours of each cell especially when the world size is relatively large. Figure 3.1 shows a similar application of Conway’s Game of Life with only 2 states of cells (dead or alive).

Figure 3.1 : Conway’s Game of Life

In this project 4 states are introduced to the cells to improve the complexity of the automata. These proposed states are, followed with their evaluation and colour:

• New Born (Old value = 0 , new value = 1) “White”
• Elder (Old value = 1, new value = 1) “Dark Blue”
• Dead ( Old value = 1, new value =0) “Violet”
• Void (Old value =0, new value =0) “Black”

This proposition takes into account of the old grid of cells as well, where as other implementations only take the current grid into account. These cell states will also be interactive in way that the user will be able to “kill” or “spawn” a cell so that human interaction is possible during evolution on run time. User will be given the option to fully randomize or partially randomize the board to observe random behaviour of the cellular automata. The implementation will also consist the classic Conway’s Game of Life with 2 states which can be activated or deactivated on run time.

Implementation

Algorithm was developed regarding the needs stated above. Outlook of the main algorithm, as well as the “handlespecialkey”,”mouseCall” and “mouseMove” functions, are shown on Figure 4.1. Figure 4.1 consists of the function names or functionalities and function descriptions shows the data it changes.

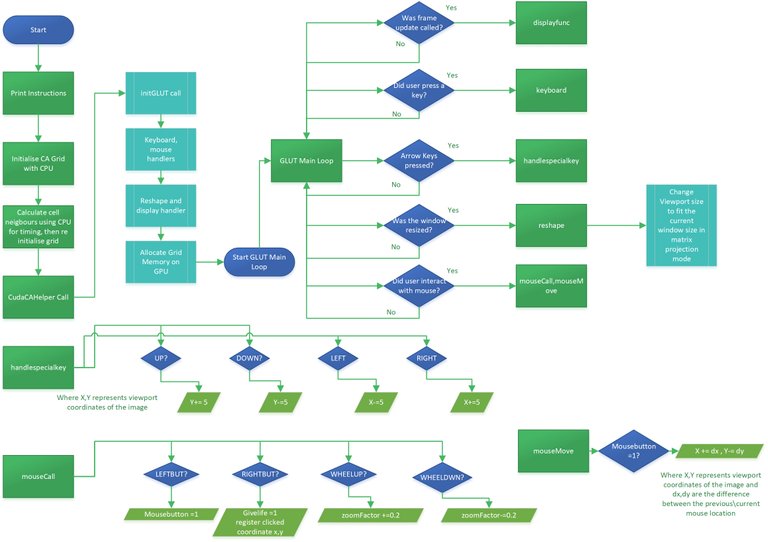
Figure 4.1: Main Overlook Flow Chart of the Algorithm

Figure 4.2 shows the key functions and processes that each function executed. Functions that are not shown in depth are explained in words instead on the left side of the relevant functions row.

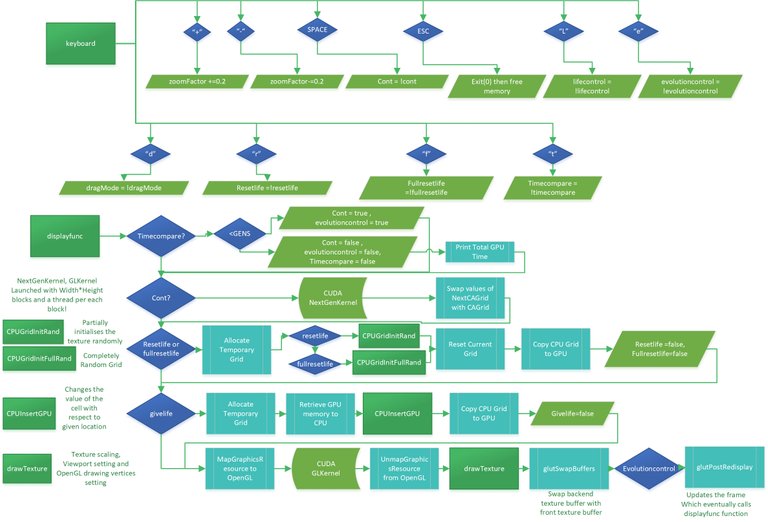
Figure 4.2: Keyboard and Display Functions Flow Chart

The user is also limited with the memory of the graphics card which depends on the width and the height of the world. Considering that the buffers use RGB channel, each cell is 64 bits on the memory meaning that 100x100 grid will take up 640000 bits (80000 bytes) or 80 kB without textures. No promises on the rendering time :)

Results

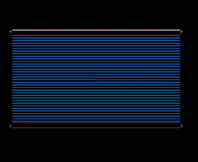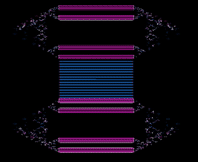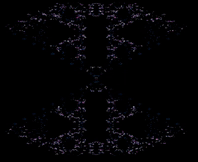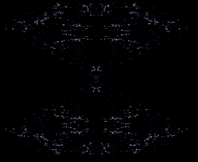
Lets start with an initial grid given below in Figure 5.1. White pixels represent alive cells and the black pixels represent "void" or empty space.

Figure 5.1: Initial Grid e=0
After 288 evolutions it becomes something like this...

Figure 5.2: Initial Grid at e=288
Some spicyness added by me to give more life and diversity

Figure 5.3 Initial Grid at e=288 with 2 states
Zooming into the middle bit which I call "the graveyard" since pink cells represent "dead" at that time...

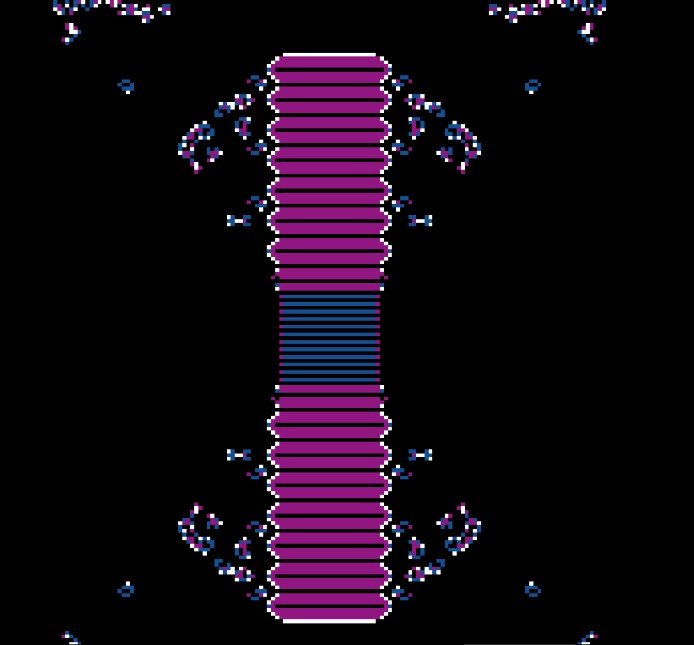
Figure 5.4 Zoomed Figure 5.2
Lets zoom in a little bit more to the lower left corner ( feels like zooming in to a galaxy if the grid is large enough :P)

Figure 5.5: Further Zoom to Figure 5.4
Then lets sprinkle some alive cells to see if they hold up ...

Figure 5.6 Spawning Cells to Disrupt Stationaries
Alone cells die, the ones spawned in the groups either kills a member and replaces it or disbands the group causing members to flee erraticly :)

Figure 5.7 : Manually Disrupted Stationary Cells at e =303
Now lets try to randomise the initial grid

Figure 5.8 Fully Randomised Grid
This is the result after 202 generations...

Figure 5.9 Full Randomised Grid at e=202

I couldn't hold my self and added some gif's. If you can't be bothered to try it out or have no knowledge in programming this would hopefully give the idea.
Initial grid to evolution
ezgif.com-crop.gif
Some zooming in
ezgif.com-crop (1).gif
Wandering around the world :P
ezgif.com-crop (2).gif

Conclusions

Project achieved the visualisation of Conway’s Game of Life with colour additions as well as other user interactions that can be executed during runtime. Additionally a function that allows the user to spawn or kill a cell during run time which can be used to create chaotic patterns. Outcome of the cellular automata was compared with Conway’s Game of Life and same patterns (periodical, stationary, glider etc..) were observed. All of the proposed functionalities are implemented and in working condition. Unfortunately, CUDA kernel that is responsible for counting cell neighbours needs to be optimized by using the explained methods to achieve faster speeds compared to the CPU. On lower end devices (Compute 3.0) frame rate is significantly low.

2DCA-CUDA

Please follow compiling directives on the source page to compile without errors.

Check 1-Dimensional Cellular Automata Encryption Project on Steem

References

[1] Stephen Wolfram. (2002). Chapter 2: The Crucial Experiment Why These Discoveries Were Not Made Before . In: A New Kind of Science. : Wolfram Media. p876.
[2] Stanford. Conway's Game of Life. Available: http://web.stanford.edu/~cdebs/GameOfLife/. Last accessed 13th April 2017.
[3] ISY, LiTH. CUDA-OpenGL Interoperability. Available: http://www.computer-graphics.se/multicore/pdf/11c%20CUDA%20and%20OpenGL.pdf. Last accessed 6th June 2017.
[4] Duane Storti and Mete Yurtoglu. (Dec 21, 2015). Live Display via Graphics Interop. Available: http://www.informit.com/articles/article.aspx?p=2455391&seqNum=2. Last accessed 6th June 2017.