In this series of post, we will derive BCH formula
BCH formula is a formula with three mathematicians, Baker-Campbell-Hausdorff
There are two definition of Lie groups as C^{\infty} and smooth manifold. Using BCH formula it turns out that these two definition are equivalent.
And for computational purpose, especially considering Universal enveloping algebra, this BCH formula plays an important role.
Let me state the form of formula
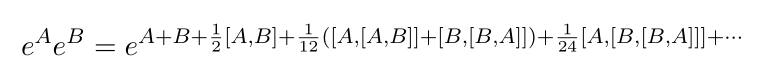
Here A,B are square matrix. In most of textbooks they compute up to 1/2 order and in some lecture notes they compute up to 1/12, here we will derive up to 1/24
Note that [A,B] = AB-BA and since we are dealing with matrix this does not vanishes.
There are many ways of deriving this BCH formula, here we will cover most elementary proof. More elegant but advanced proof can be found in wiki
The strategy here is expand
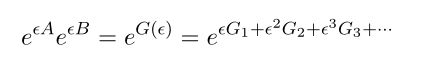
and compute the coefficients G_1, G_2 and so on. The computation results for these coefficients are following
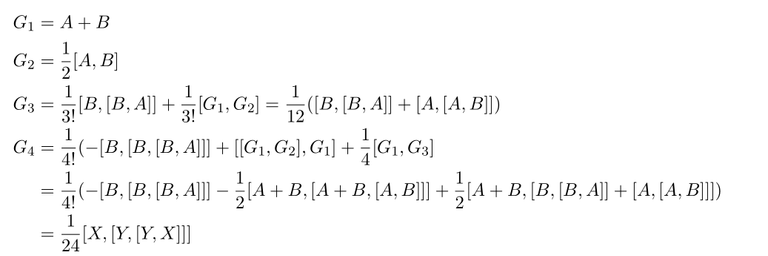
To derive this let's do study some elementary computation on matrix.
Some basic equations
Expression of exponential for matrix
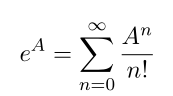
Differentiation of matrix
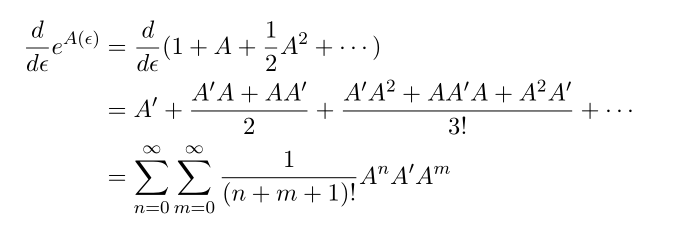
The important fact here is A' and A does not commute.
And from A A^{-1} = I, we have
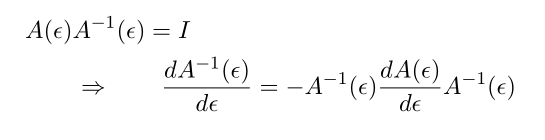
this show how the differenitation of A^{-1} with respect to epsilon is related with differentiation of A with repsect to epsilon.
Next, we need
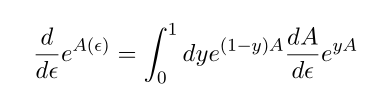
Let's try to derive.
L.H.S are already cover in the above, so Let's compute R.H.S
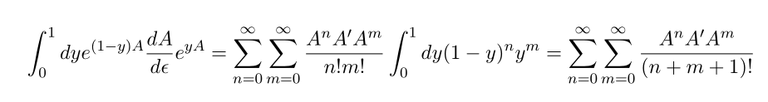
Here we used
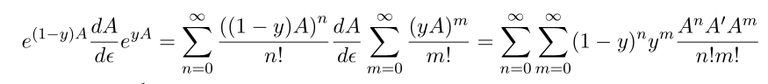
and beta function .
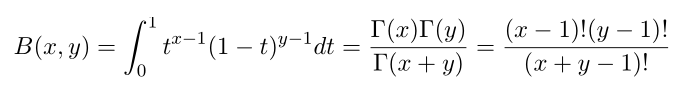
Now we need
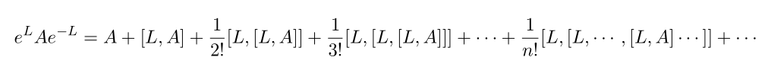
Here L, A are square matrix of same size.
Now let's derive this
From
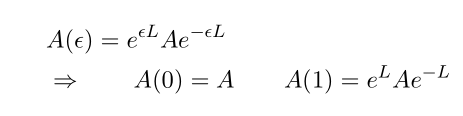
by differentiation with respect to epsilon many times we have
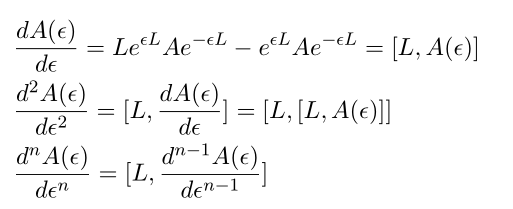
using this we have
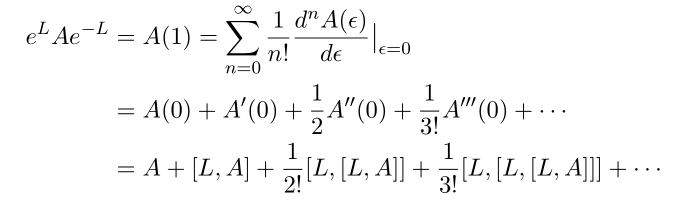
Now basically we are done.
In the next post using above equtions we will derive BCH formula.
too tough for me. maybe next post will be easy :)
very nice post
The history of the Baker-Campbell-Hausdorff (BCH) formula began in 1890 and involves Schur, Campbell, Poincaré, Baker, Pascal, Hausdorff, Yoshida and Dynkin. For real numbers we have z = log (exp (x) exp (y)) = x + y. However, matrices for Z = log (exp (X) exp (Y)) ≠ X + Y, except when they switch [X, Y] = XY-YX = 0. The formula BCH has infinite terms, although in many applications is truncated by a finite number of them.
Yes,
And there are many ways to derive BCH formula.
In this post, using only some basic method, i.e., taylor expansion and integration by parts, I will derive BCH formula. [Of course there are much elegant way to prove this formula, as i cite in wiki and many standard Lie group textbooks]
Also, In the near future, I'd like to post about Dynkin diagram.