Following from last posting baiscs, at this time we are going to derive
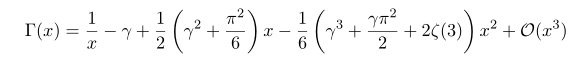
this equation and do some application.
First from recursive relation of gamma function, i.e., Gamma(z+1) = z Gamma(z), we have
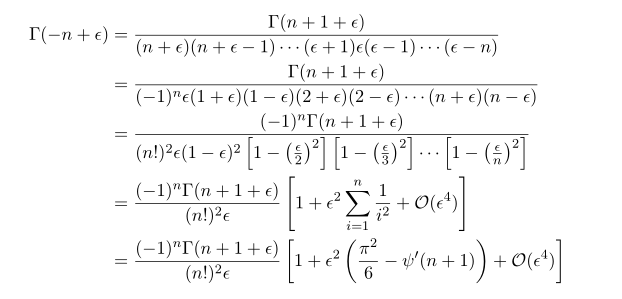
This is a usual textbook approach for some negative factorials. Using the formula in the previous post
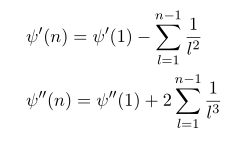
with the gemoetric series, 
by collecting terms of epsilon^2 in the denomiantor, we can easily obtain above equation.
The next thing to do is taylor expansion about Gamma(n+1+epsilon) about the parameter epsilon.
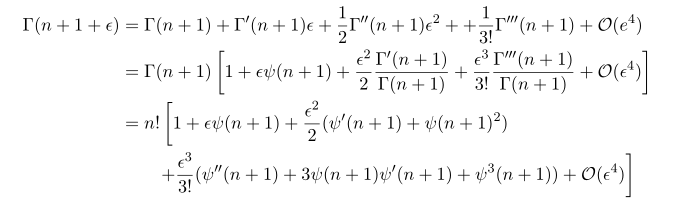
In the process we used
which we derived in the previous post.
Now just plugging these results we have
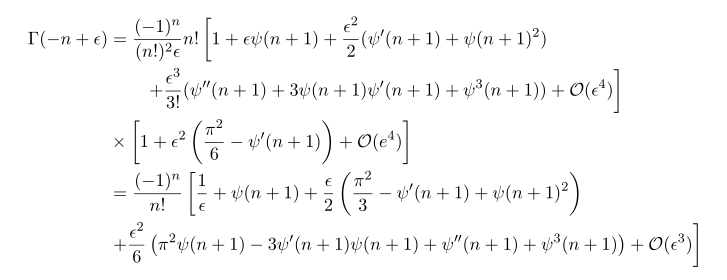
Note that upon here we computed upto order 4 of epsilon, but you can see that there is another epsilon in the denoimnator so in this computation we obtain at most order 3 of epsilon. To compute more higer terms we need to compute more higher orders.
Now we are left with plugging n=0 and re-ordering. Using the values of psi(1), psi'(1), psi''(1) which we derive in previous post
by plugging these, we have
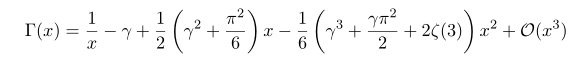
Which is desired results.
Application
With the combination of complex integration we do more than that.
First state some formula about complex integration
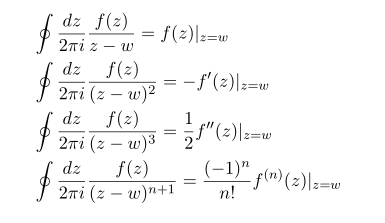
From
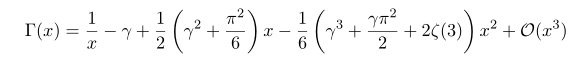we have
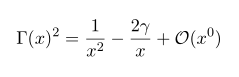
In case of no pole, contour integral vanishes, so for arbitrary function A(z), we can do
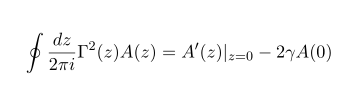
In this way we can use gamma fucntion and do the integration more easily. For another type of special function, like beta function or generalized gamma function, etc., you can do the similar things!.