Consider the following calculation:
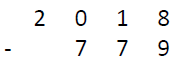
In elementary school, I was taught to solve this kind of problem by borrowing tens to fill in the missing ones, hundreds to fill in missing tens and so on:
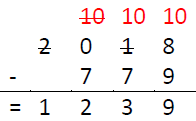
This method is annoying in cases where you have to do a lot of borrowing, so I came up with an alternative approach. Whereas subtraction from a number like 2018 is likely to involve some borrowing (since 2, 0 and 1 are low digits), the number 999 never will. Therefore, let’s split up the previous problem like this:
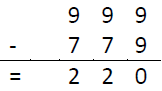
This subtraction is much faster to make than the previous one, but now we need to add the difference between 2018 and 999. Fortunately, we don’t have to think hard to find this difference: simply subtract one from the first digit in 2018 and add one to the last:

Then, do the addition:

Problem solved! Here’s the general two-step procedure for subtracting a number y from a number x:
1: Subtract y from a number consisting of as many 9’s as the number of digits in x, minus 1. Don’t waste time writing out every 9; just use a shorthand like this:

2: Add the result to the number x from which you’ve lowered the first digit by 1 and increased the last digit by 1.
If you’re accustomed to the classic method I mentioned at the beginning, you might not find my approach to be faster right away. However, it is advantageous in calculations where x and y are large, and y has higher digit values than x.
Here’s a full solution to a subtraction problem, with x=210323 and y=89669:
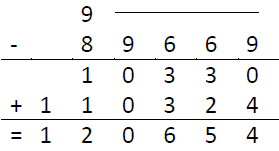
Do you know a better method for doing subtractions by hand? Please let me know!
Beautiful. This certainly is more efficient for examples like the one you've shown (2018 - 779), but what about (2018 - 9)? I wonder what method is the most efficient on average.
If forced to write out the steps, then the old method is definitely faster for an example like 2018 - 9. But I would argue that you shouldn't require any algorithm to solve that one ;).
For typical elementary school puzzles, the difference in effort required to carry out the calculations is negligible, in which case the old method may be preferable, because it's more obvious from the writing what is going on. As the number of digits increase, I believe the amount of extra time required increases less with my method.
I wodered that because I was thinking about more efficient ways to write programs that perform arithmatic.
Key word borrow equals usery ! We were taught wrong to begin with !But I see a lot of us are waking up ! I you have some time check up on my post on why the Computer Keyboard Is Dead !