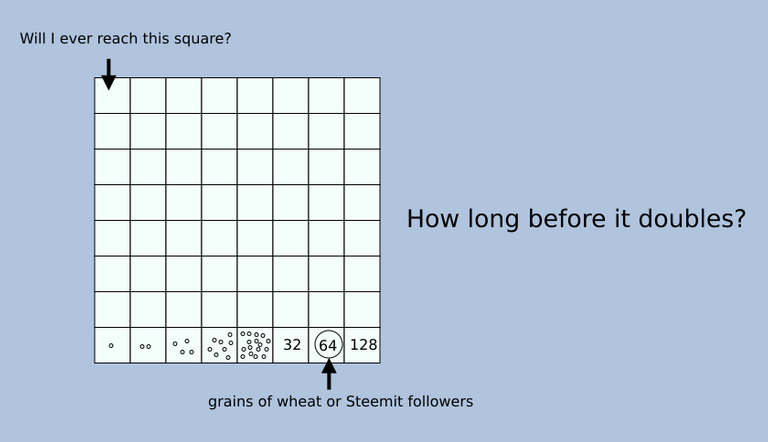
There is a fable I once heard about someone who asks for a payment in wheat. The amount of wheat is determined thusly: on a chess board with 64 squares, place on the first square 1 grain of wheat, 2 grains on the second square, 4 on the third, and so on, doubling the amount of grain for each square. It doesn't seem at first that this will require much grain, but human intuition here is deceiving. By the 64th square, you will have placed 18,446,744,073,709,551,615 grains of wheat. (See Wikipedia for details.)
At the time of this writing I have 64 followers, a nice power of 2. The question is: how long will it take me to double this number? And double it again. And again. This leads to the next question: will doubling this number require the same amount of work that I've already done, or will it somehow require less work?
Here's my guess: it will require somewhat less work the second time. Why? There are many reasons:
- I'm getting better at what I do. Practice makes perfect, and I'm not perfect yet.
- Network effects: the more followers I have, the more likely other people will re-Steem my posts or at least mention me in their posts.
- Luck: I'm bound to get lucky from time to time.
- The snowball effect or positive feedback loop. The more successful I am, the more successful I will want to be, the harder I will work, the more successful I will be. . . Repeat loop forever. In other words, success breeds success, which breeds more success, which breeds even more success. . .
Of course, this does not mean that gaining followers has a reliable "doubling time." Doubling time will probably decrease for a while, slowly get to diminishing returns, and then start to increase exponentially. Too bad for me, but good for Steemit as a whole.
I have started to notice that after the 200 mark the numbers started to roll in faster. Not sure why. Maybe people needed to see my staying power or something. That is just a bias observation on my end though.
Good to know.
How about trying to test if your hypothesis is true?
Time will tell.