Difference between first and second order systems:
A first order system quickens or slows its response based on its parameter, while a second order system also changes the entire form of the response based on its parameters.
An example of a first order system:
(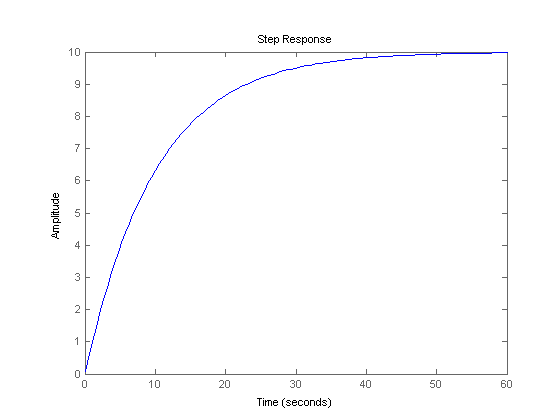 )
)
(A first order system, response to a step input)
The primary parameter of a first order system is the time constant, often written as τ.
There are three different forms of response for a second order system: a underdamped, overdamped, and critically damped response.
(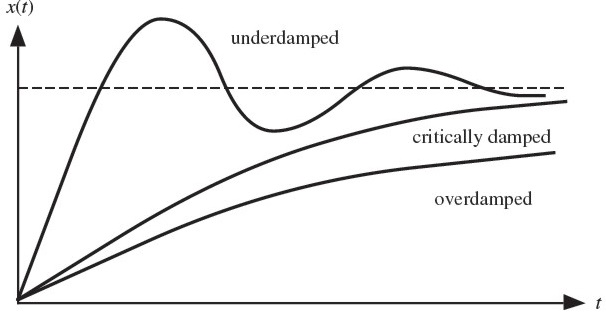 )
)
(A second order system, response to step input. Another response, undamped, is not on the image but looks like a sine wave. (It doesn’t settle.) The dashed line represents steady state. The response approaches the steady state value as t grows larger.)
The parameters of a second order system are the natural frequency ωₙ, and the damping ratio ζ.
The lower ζ, the more the response varies like a sine wave. A higher ζ gives a smoother decay response. The form changes at ζ = 1. At ζ = 1, the form is critically damped.
Notice that the overdamped and critically damped responses look similar to a first order response. In fact, their functions are similar as well:
First order response:
x(t) = 1-e⁻ʳᵗ
Second order response:
Overdamped
x(t) = C₁(e⁻ʳᵗ) + C₂(e⁻ˢᵗ)
Critically damped
x(t) = C₁(e⁻ʳᵗ) + C₂(te⁻ˢᵗ)
These responses depend on exponential decay. In an overdamped response, the time constants, τ₁ and τ₂ are the reciprocals of r and s (which are 1/r, and 1/s). An overdamped response means that the damping ratio, ζ, is greater than 1, but a critically damped response means that the damping ratio is exactly 1. Interestingly, you can approximate a critically damped system by letting ζ =0.9999 or ζ=1.00001 .
Underdamped
x(t) = C₁(e⁻ᵈᵗ)cos(ωd - ϕ)
The damped frequency, ωd, is related to ωₙ by the damping ratio, ζ.
ωd = ωₙ*sqrt(1 - ζ²)
An undamped system can be quickly analyzed with a few numbers. Here’s how to find the peak time, settling time, percent overshoot, and rise time.
Peak Time
The peak time, Tₚ, is the time it takes for the system response to reach the first peak. The first peak should also be the maximum, so the peak time can be found from the damped natural frequency
Tₚ = π/(ωd) where, again, the damped natural frequency is
ωd = ωₙ*sqrt(1 — ζ²)
Settling Time
The settling time, Tₛ, is the time it takes for the system to stay within 2% of steady state. By this time, the system response has leveled off and is not changing much.
Tₛ = 4/ζωₙ
Overshoot
The overshoot, Oₛ, is the amount the system response ends up going over the steady state amount. If your system levels off at 1, but peaks at 1.1, than your overshoot is 0.1 and your percent overshoot is 10%.
Oₛ = (peakᵥₐₗᵤₑ-steady stateᵥₐₗᵤₑ)/steady stateᵥₐₗᵤₑ
(multiply by 100 for percentage)
An equation for overshoot is:
Overshoot percentage = 100 * e ^ - (πζ / √(1 — ζ²) )
Rise Time
The rise time, Tᵣ, is the time that the system response takes to go from 10% to 90% of the steady state value. For example, if that steady state value is 2, than find the times at which the system response is 0.2 and 1.8, and find the difference.
Hi! I am a robot. I just upvoted you! I found similar content that readers might be interested in:
https://ocw.mit.edu/courses/mathematics/18-03sc-differential-equations-fall-2011/unit-ii-second-order-constant-coefficient-linear-equations/damped-harmonic-oscillators/MIT18_03SCF11_s13_2text.pdf