Hi there. This math post features some trigonometric identities (on right angle triangles) with math proofs.
Math text are displayed as images through the use of QuickLaTeX.com.

Review Of SOH CAH TOA & Reciprocal Trigonometric Functions
Given an angle 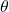 (theta) the trigonometric functions represent ratios of the side lengths of a right angle triangle.
(theta) the trigonometric functions represent ratios of the side lengths of a right angle triangle.
To save space, refer to the summary image below. (a = adjacent side length, o = opposite side length, h = hypotenuse length)

Note that when it comes to fractions, the denominator (bottom of a fraction) cannot be zero. Furthermore, angles which would make the denominator zero are not permitted.
These trigonometric functions can be used in the xy coordinate system as shown in the image below. The angle is theta, the adjacent side to theta is x, the opposite side to theta is y and the hypotenuse is the radius. A unit circle of 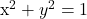 (where r = 1) is assumed.
(where r = 1) is assumed.
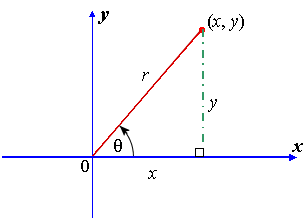
The six trigonometric functions now become:
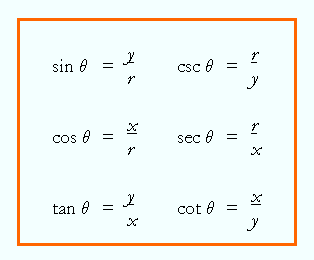
Screenshot Image From http://www.themathpage.com/aTrig/unit-circle.htm
The bottom part of the fraction cannot be zero.
A Few Trigonometric Identities With Proofs
Here are a few trigonometric identities with proofs. It is assumed that the angle theta is from 0 to 360 inclusive.
Example One

The cotangent of an angle is 1 divided by the tangent of the same angle. With this in mind, the left side of the equation can equal one as follows:

An alternate way is using  .
.
Proofs of  are done similarly.
are done similarly.
Example Two

To start, we use the fact that  and
and  . The left side of the above equation becomes:
. The left side of the above equation becomes:

r is the radius of a circle. Using this idea, will turn the fraction into 1.What completes this proof is knowing that the top of the fraction is actually the equation of the circle. That is, 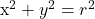 where
where

Example Three

The tangent of an angle is  . This fraction would be squared and a common denominator needs to be determined.
. This fraction would be squared and a common denominator needs to be determined.

Notice how the top of the fraction is the equation of the circle. This fact is used again along with exponent rules. The resulting ratio is the square of the secant of the angle.

Example Four

The cotangent of an angle is  With a substitution and algebra, once can obtain the right side of the above equation.
With a substitution and algebra, once can obtain the right side of the above equation.

References
http://www.sosmath.com/trig/Trig5/trig5/trig5.html
Functions 11 by Nelson Thomson
fyi. Your brackets would look better if you put left/right markers on them in the latex: {\left( \frac{x}{y} \right)}^2
Okay. Fixed. Thank you for the tip.
excellent explanation friend already you vote, greetings