Hi. In this math post, the focus is on number factors. This topic is useful for those at around grades six to ten. Number factors are helpful for division, and the algebra method of factoring.
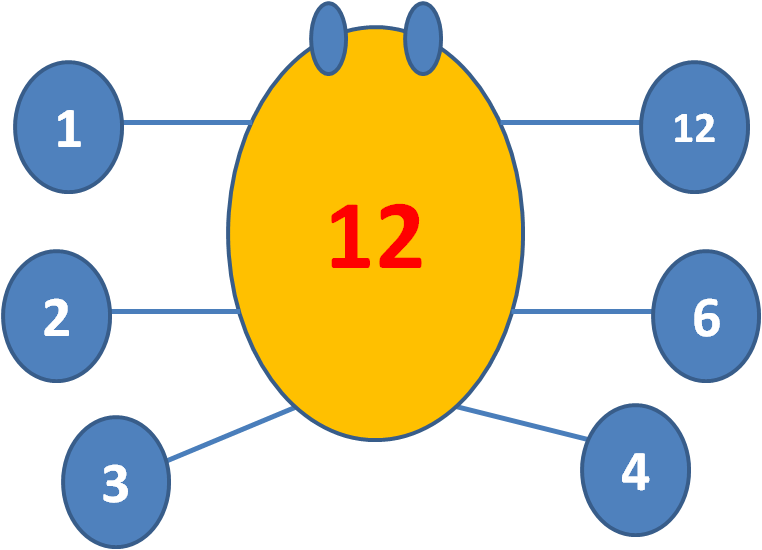
Table Of Contents
What Is A Factor?
Examples of Number Factors
Prime Numbers & Prime Factorization
Practice Problems
Answers
References
What Is A Factor?
A number factor is a positive whole number which (exactly) divides into another whole number with a zero remainder. In other words, a whole number divided by a factor gives another whole number. As an example, any even number can be divided by 2 with zero remainder.

Examples of Number Factors
Here are some examples.
The number 6 has factors of 1, 2, 3 and 6 itself. These factors divide into 6 exactly since 6 ÷ 1 = 6, 6 ÷ 2 = 3, 6 ÷ 3 = 2, and 6 ÷ 6 = 1.
The number 15 has factors of 1, 3, 5, and 15 itself. We can have 1 × 15 = 15, and 3 × 5 = 15. Alternatively, we can show that 15 ÷ 1 = 15, 15 ÷ 3 = 5, 15 ÷ 15 = 1, and 15 ÷ 5 = 3.
Factors are not restricted to numbers. We can use variables such as xx. As an example, factors of  are 1, and
are 1, and  itself.
itself.

Prime Numbers
If a whole positive number has two factors which are 1 and itself, this number is considered as a prime number. Examples of prime numbers include 2, 3, 5, 7, 11, 13, and 29.
Prime Factorization
Any positive whole number greater than one has number factors which are prime numbers. As an example, the number 42 can be written as:

Practice Problems
What are the factors of the number 12?
What are the factors of the number 49?
What are the factors of the number 35?
Is 31 a prime number? Why?
What are the factors of
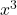
What are the factors of

Find the prime factors of the number 60.
Answers
1, 2, 3, 4, 6 and 12
1, 7, 49
1, 5, 7, 35
The factors of 31 are 1, and 31 itself. It is a prime number.


References
I used http://www.quicklatex.com/ and http://math.typeit.org/ for math text/images.
Yay math :D
Thanks for sharing :)
Wow! Nice explanation! I aslo like math!
Very nice visualisations!