
Para entender qué es el código binario, antes tenemos que saber qué son los número binarios.
Los números binarios son todos aquellos números formados por 0's y 1's, es decir: 101, 11111, 1000011, etc etc etc
Los números que se utilizan día a día para contar, en el calendario... vamos, los númros normales, son números decimales, es decir, números compuestos de dígitos del 0 al 9: 141341, 92921, 4552. Estos son los números que todos conocemos.
Pero, ¿para qué vale esto de los números binarios? Mucha gente sabrá que las máquinas utilizan codificación binaria para funcionar, para comunicarse, para enviar mensajes, etc. Esto se debe a que las máquinas están compuestas de componentes electrónicos, magnéticos, componentes elécticos que pueden estar o encendidos o apagados.
¿Sabéis ya por donde voy? Cuando el componente está encendido correspondería a un 1, y cuando está apagado, corresponde al 0. Parece fácil, ¿verdad? No lo es tanto. Con estos dos números, las máquinas se tienen que apañar para enterderlo todo: números, colores, textos, posiciones, etc etc etc.
Esto es posible porque todo color, toda letra, todo número, tiene su representación en número decimal y luego ese número decimal, se puede convertir a número binario.
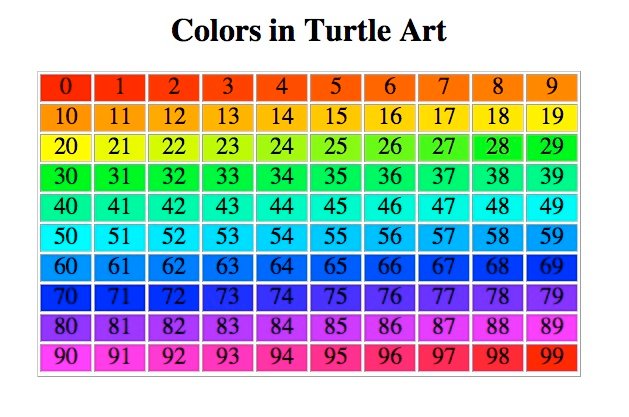
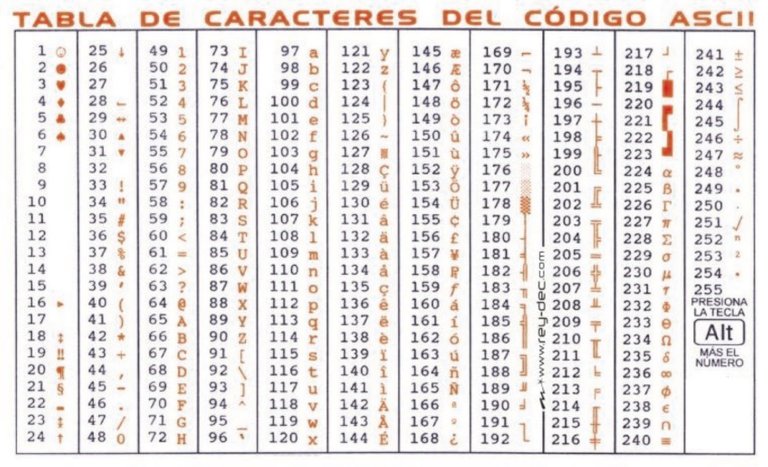
Ahora bien, para entender cómo funciona el sistema binario, y cómo pasar de un número decimal a un número binario y que nuestro ordenador se entere de lo que le queremos decir, debemos entender como funciona nuestro sistema decimal.
Pongamos el número 524. En el colegio nos enseñaron que el 4 está en las unidades, el 2 en las decenas y el 5 en las centenas. Esto quiere decir que el 4 vale 4, el 2 vale 20 y el 5 vale 500. Los tres números juntos en ese orden forman el 524.
Pero, ¿por qué el 4 vale 4, el 2 vale 20 y el 5 vale 500? Eso de debe a la posición de derecha a izquierda que tiene el dígito en el número. Es decir, como se trata de un sistema decimal, cada columna o cada posición, vale 10 veces más que la columna o posición de su derecha.
10000 1000 100 10 1
5 2 4
Ahora si multiplicamos el valor de cada dígito por el valor de cada columna y sumamos las columnas, nos daría el número 524.
4 x 1 + 2 x 10 + 5 x 100 = 4 + 20 + 500 = 524
Pues ahora que ya entendemos esto, el sistema binario es exactamente igual, sólo que las columnas en vez de valer 10 veces el valor de su derecha, vale solo 2.
512 256 128 64 32 16 8 4 2 1
1 0 0 0 0 0 1 1 0 0
Si ahora multiplicamos cada dígito binario por el valor de su columna y luego sumamos las columnas, obtendremos 524 y sabremos que el número 1000001100 corresponde al número 524 en binario.
1 x 512 + 0 x 256 + 0 x 128 + 0 x 64 + 0 x 32 + 0 x 16 + 1 x 8 + 1 x 4 + 0 x 2 + 0 x 1=
512 + 0 + 0 + 0 + 0 + 0 + 8 + 4 + 0 + 0 = 524
Ahora que ya sabemos esto, podemos poner con números binarios cualquier cosa que se nos ocurra. Lo único malo, es que ocupan más, pero es la única forma de hacer que nuestros ordenadores se enteren :)
Muy interesante y bien explicado :D
Muchas gracias :)
Buen aporte
Muchas gracias :)
Congratulations @frmjar! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPSTOP