Desde la aparición del famoso texto de Hardy, Lttlewood and Paley, titulado Inequalities, las desigualdades han sido objeto de estudio por la comunidad científica matemática. Muchos otros autores han escrito sobre el tema, y algunos otros sobre la aplicabilidad de este tópico en diversas ramas de la ciencia como Física, Ingeniería, Investigación de Operaciones, y otras más.
Hay una en particular, sencilla e interesante a la vez.
válida para cualesquiera valores númericos positivos a y b
Veamos una prueba de que esto es cierto.
Prueba
Dado que a y b son números reales positivos entonces podemos asegurar que
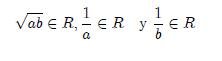, y por lo tanto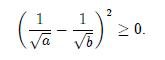
Usando la suma de fracciones vemos que
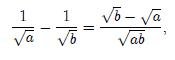
entonces se tiene que
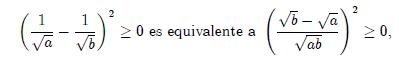
A partir de esta última, y usando propiedades de la potencia obtenemos que
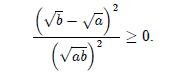
Se deduce que
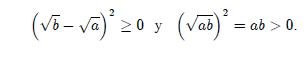
Desarrollando el cuadrado de la diferencia obtenemos que
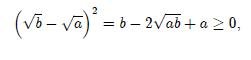
y a partir de esto que
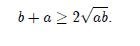
Usando propiedades de las desigualdades y recordando que a y b son números reales positivos, tenemos que
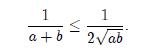
Racionalizando el lado derecho de esta desigualdad obtenemos
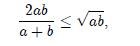
y esta expresión es equivalente a
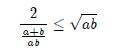
la que, a su vez es equivalente a
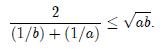
la cual es la desigualdad buscada. (Fin de la prueba).
Básicamente, la prueba de la validez de esta clásica y sencilla desigualdad se fundamentó en la axiomática de los números reales y las propiedades de las potencias.
Espero que sea de utilidad esta publicación. Quiero por medio de ésta y otras a futuro motivar e introducir a interesados en una nueva área de investigación en Matemáticas que hace uso de las desigualdades y un concepto generalizado de convexidad de funciones que en los últimos años se ha ido desarrollando.
Saludos , desde Venezuela.
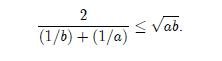
Un valioso aporte y asi como ésta existen algunas otras cuya demostración no es muy evidente para algunos estudiantes y en oportunidades puede retrasar su estudio
@jorgehh, thank you for supporting @steemitboard as a witness.
You can click on your award to jump to your Board of Honor
Once again, thanks for your support!