Hello friends of steemit
For this opportunity I will talk about the combinatorial numbers, in my previous post made several days ago explain how to arrive at the combination expression, starting from the meaning of the variations and permutation, denoted as follows:
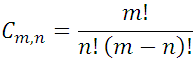
Because of its origin, it is usually called combinatorial numbers and also binomial coefficients, because they have special importance in the development of the powers of the form (a + b) m , to represent them Euler used the symbol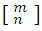 
, but nowadays the notation 
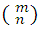is more frequent, which leaves us by definition:
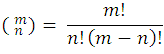
Some fundamental properties of the combinatorial numbers are the following:
The number
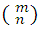, is always integer, in effect as this number equals C m,n , and since this is integer, since it is the number of combinations of m elements taken n to n, so is the first.The number
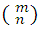is equal to the number 
. In fact, by definition, you have to:
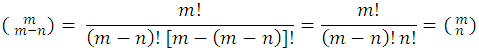
Potency of a Binomial
As an application of the combinatorial theory that we have just mentioned, I will explain below the formula that expresses the development of the power of a binomial, generally known as the formula of Newton's binomial formula.
Successive potency of (a + b)
Following the ordinary rule of multiplication, we can verify that :
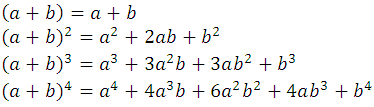
Similarly, it will be obtained for exponents 5, 6, etc., but as this procedure becomes more and more laborious, it is convenient to find a training law for these powers. Indeed, it can be observed that each of the developments are homogeneous polynomials, complete ordered and of the same degree as the power of the corresponding binomial, so the developments that are obtained from the following powers will be of the same nature. Also, as the exponents of a and b in any of the developments, that of (a + b) 4 . for example, they appear in the following order:
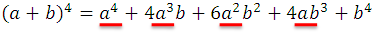
The exponents of a marked with the red color: 4, 3, 2, 1, 0, decrease from 4 to 0, remember that we can assume that the last exponent of a is 0 for the property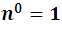 
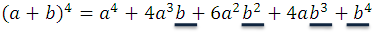
The exponents of b marked with the blue color: 0, 1, 2, 3, 4, grow from 0 to 4, if the developments follow this pattern, it can be easily deduced that the next exponent 5, for example, it comes as follows:
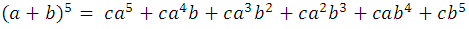
where c, are the coefficients of development, we can generally write it as follows:
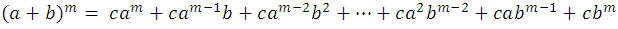
Development coefficients (a + b) m
It is quite understandable that it is enough to find the formation of the coefficients, to have the law of formation of development. Looking at the coefficients of the first of the first exponents:
Coefficients of (a+b): 1, 1. That can very well be written using the notation for the combinations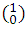 
and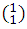 
is say, the results of the combinations correspond to the coefficients of the exponent 1 development, analogously
Coefficients of (a + b)2: 1,2,1, which in combination form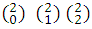 
Coefficients of (a+b) 3 : 1,3,3,1 =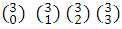 
Coefficients of (a+b) 4 : 1,4,6,4,1 =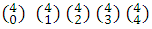 
So we could build the developments successively, which generally remains:
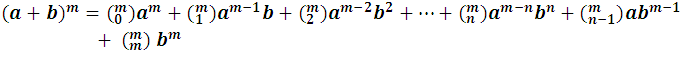
This last development is usually called Newton's formula or Newton's binomial, which in its compact form:
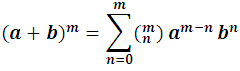
In summary, we can say that the development of the bth power of the binomial (a+b), being m integral and positive, is a homogeneous, complete and ordered polynomial of degree m in the letters a and b, whose coefficients are the combinatorial numbers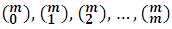 
For example:
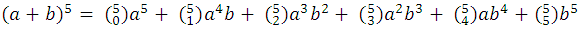
With this I finish the explanation of the binomial of Newton and its easy deduction, I hope that this basic but important information will be of help for you my dear steemians
bibliography:
http://www.cimat.mx/~jortega/MaterialDidactico/EPyE09/Cap2.pdf.
http://www.ub.edu/stat/GrupsInnovacio/Statmedia/demo/Temas/Capitulo1/B0C1m1t13.htm
by @juancmz