Consider a rectangle ABCD and a parallelogram EFGH with the same base length and height.
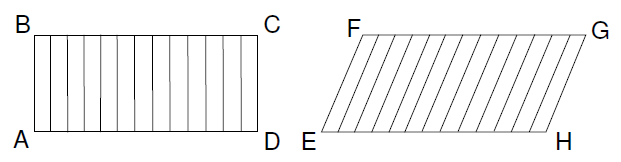
Let us cut the rectangle ABCD into infinitely many infinitely thin strips: lines, which fill the whole area of the rectangle. Similarly, we can cut the parallelogram EFGH into infinitely many lines which also completely fill its area.
Note that the base lengths (AD and EH) of the two shapes are equal, hence the quantity of lines in the two shapes is the same - every line in the rectangle has a corresponding one in the parallelogram. All the lines in the parallelogram are, however, longer than those of the rectangle, and must thus all cover a greater area together.
Consequently, the area of the parallelogram is greater than the area of the rectangle.
For other sophisms check out my other posts.
Stop confusing me
The path to clarity and enlightenment lies through thick fog of confusion!
What is the chance Im currently watching The Mist on Netflix :)