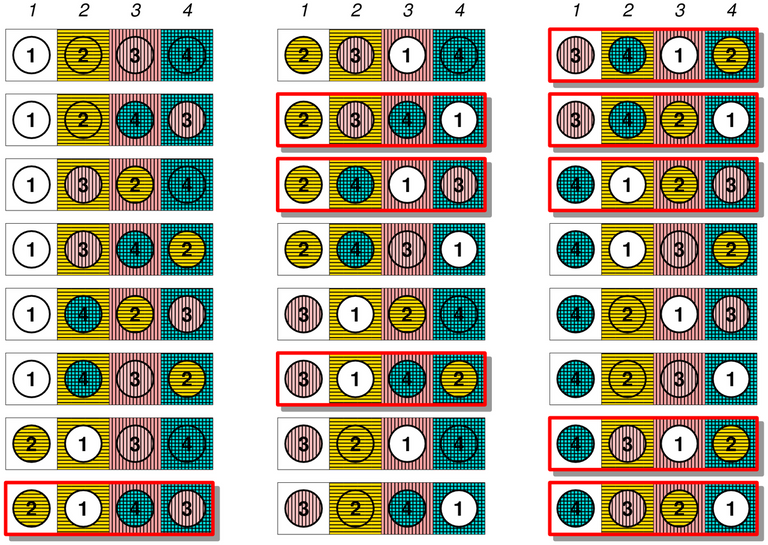
[1]
0. What is a Derangement?
In mathematics, permutation is an act of arranging all the members of a set into some sequence or order. A permutation which leaves no element fixed is called a derangement . In many cases, we deal with 

So, put another way, a derangement of 


For example, 


Let's look at one more example 
| Element | 1 | 2 | 3 |
|---|---|---|---|
| maps to | 2 | 3 | 1 |
| maps to | 3 | 1 | 2 |
In general, we need to ask the question:
 different permutations of
different permutations of  distinct objects, how many leave no object in its original place?
distinct objects, how many leave no object in its original place? The answer to the question will provide a general formula for 

the probability that a permutation of 
1. Old but Gold Recurrence Relation
Viewing 






If a permutation

is a derangement, then it must be that &space;\neq&space;1)

&space;=&space;k&space;(>&space;1))
Now there are two possibilities.
1. If &space;=&space;1)

and there are exactly
 of these.
of these.
2. If &space;\neq&space;1)

to

with a restriction &space;\neq&space;1)

to

if 


Since our choice of 
(D_{n-1}&space;+&space;D_{n-2})\&space;(n&space;\geq&space;3))
Clever trick is to divide both sides by 
D_{n-1}}{n!}&space;+&space;\frac{(n-1)D_{n-2}}{n!}&space;\\&space;&=&space;\frac{D_{n-1}}{(n-1)!}&space;\left(1-&space;\frac{1}{n}&space;\right&space;)&space;+&space;\frac{D_{n-2}}{(n-2)!}&space;\cdot&space;\frac{1}{n}\\&space;\iff&space;p_n&space;&=&space;\left(1-&space;\frac{1}{n}&space;\right&space;)&space;p_{n-1}&space;+&space;\frac{1}{n}&space;\cdot&space;p_{n-2}&space;\\&space;\iff&space;(p_n&space;&-&space;p_{n-1})&space;=&space;-\frac{1}{n}&space;(p_{n-1}&space;-&space;p_{n-2})&space;\end{align*})
Defining 
&space;\times&space;\left(&space;-\frac{1}{n-1}&space;\right&space;)&space;\times&space;...&space;\times&space;\left(&space;-\frac{1}{1}&space;\right&space;)&space;\\&space;&=&space;(-1)^{n}&space;\frac{1}{n!}&space;\end{align*})
so that
^{i}\frac{1}{i!})
with
^{i}\frac{1}{i!}&space;\right))
2. The other way around
[2]
We've established the formula for derangement, but there is a more intuitive way of relating the total number of permutations 

We can count the total 


where 






so that

This simple looking relationship is indeed very useful, as we will use in further sections.
3. Expected Number of Fixed points
A rather paradoxical situation arise when we calculate the expeced number of fixed points. Suppose that we perform the experiment of matching the initial arrangement 



So the expectation is nothing but
)
In the previous Section, we already obtained the formula for )
&space;=&space;\frac{|T_{n-r}|}{n!}&space;=&space;\frac{\binom{n}{n-r}&space;D_{n-r}}{n!})
Now, straightforward calculation gives
&space;\frac{\binom{n}{s}D_s}{n!}\&space;(\because&space;s&space;=&space;n-r)&space;\\&space;&=&space;\sum_{s=0}^{n-1}&space;\frac{D_s}{s!(n-s-1)!}\&space;(\because&space;n-n=0)\\&space;&=&space;\frac{1}{(n-1)!}\sum_{s=0}^{n-1}&space;\binom{n-1}{s}D_s&space;\end{align*})
Since
!)
by our previous result in Section 3, we get

regardless of 
How should we interpret this weird result? Many of us tend to think the expected number of fixed points will grow as 


This will help you understand what's going on more clearly. Consider a random variable 


&space;=&space;\frac{1}{n}&space;\times&space;n&space;=1)
so that 
4. Asymptotic Property of derangement
[3]
Finally, one can ask that
 as
as  gets large?
gets large? This is nothing but asking the limit
^i&space;\frac{1}{i!})
one can easily show that the limit actually exists, and surprisingly, using the well known fact
)
gives 
Also one can ask that
) as
as  gets large?
gets large? Recall that we defined random variable 
&space;=&space;\frac{\binom{n}{n-r}D_{n-r}}{n!}&space;=&space;\frac{1}{r!}&space;\cdot&space;\frac{D_{n-r}}{(n-r)!})
We already proved that !}&space;\rightarrow&space;\frac{1}{e})
&space;\rightarrow&space;\frac{e^{-1}}{r!})
5. Computer Simulation
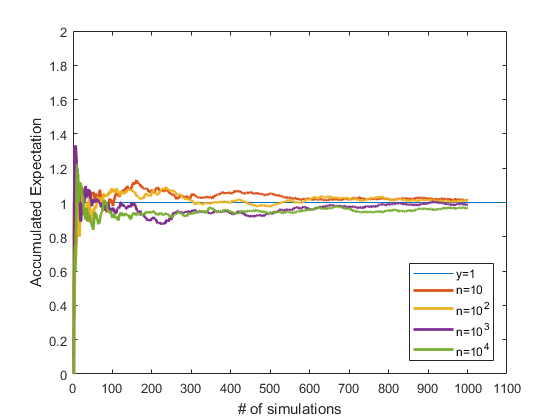
5-1. Expected number of fixed point revisited
Here is the MATLAB simulation for accumulated expectation of number of fixed points for various 

5-2. Asymptotic property of Derangement revisited
Now here is the MATLAB simulation for 
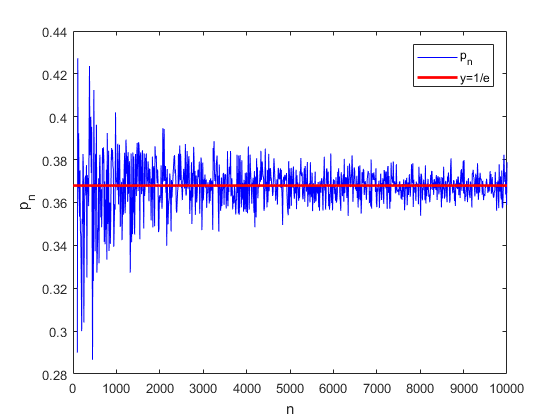
You can see it clearly converges to 

6. Conclusion
Number of derangement of
items is equal to
The expectated number of fixed points in single random permutation is 1, regardless of
.
The probability of having derangement converges to
.
7. Citations
[1] Image Source Link, By RokerHRO - Own work, CC BY 3.0
[2] Julian Havil, Nonplussed! Mathematical Proof of Implausible Ideas. Chapter 5 page 53
[3] Julian Havil, Nonplussed! Mathematical Proof of Implausible Ideas. Chapter 5 page 56
MATLAB plots are self-made.
^r}{r!})
Congratulations @mathsolver! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPThis post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Hi @mathsolver!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV