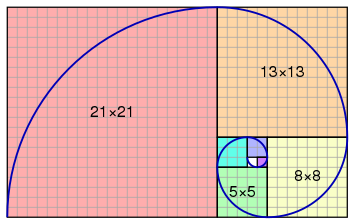
[1]
Relationship between Fibonacci numbers
1. The History
We all know what Fibonacci sequence is, but to be sure, let's just state the full recurrence relation here. A Fibonacci sequence is collection of integers 
)
First few terms of Fibonacci sequence are

The sequence first appeared on the book Liber Abaci by Leonardo of Pisa (known as Fibonacci). Fibonacci posed an idealized growth of rabbit population as follows.
A single pair of rabbits (one male, and other one female) born.
Rabbits are able to mate at age of 1 month, and 1 month after the mating, female produce another pair (also one male and other one female) of rabbits.
Rabbits never die nor stop mating so that every pair of rabbits produce their offspring indefinitely.
Then the question Fibonacci proposed was
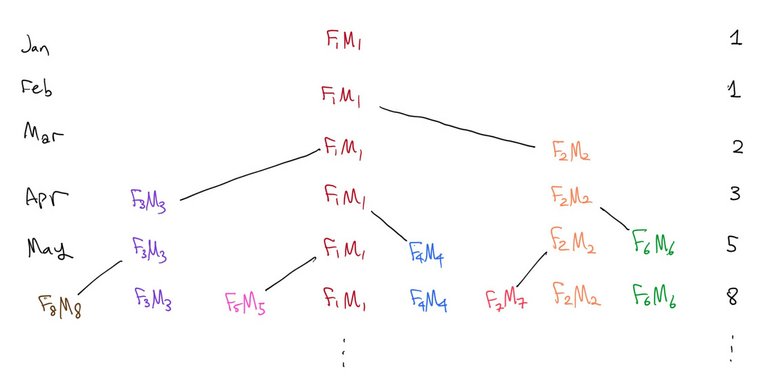
Clearly, the total number of rabbit pairs in 

)

given that 

What I like to talk about in this post is not the implementation of Fibonacci sequence in real world, but the relationship between the terms in Fibonacci sequence; 
2. Greatest Common Divisor of Fibonacci numbers
The goal of this post is to find the greatest common divisor of two fibonacci numbers,
)
First let's look at some examples.
If we take
, then
. Woops! the greatest common divisor is nothing but
.
If we take
, then
, so that
If we take
, then
so that
(relatively prime).
As you can see, the greatest common divisor of two fibonacci numbers is also another fibonacci number. Is this mere coincidence? Well let's find out.
3. Clever Identity
First, let's use matrix to represent the recurrence relation. Define a 2 by 2 matrix

for 


so that

Since 


using iterated multiplication of square matrix. Now, here comes the clever trick. Put 


The matrix multiplication is associative, so that

Using closed form expression for 

or equivalently,

Comparing )

This simple looking relationship is indeed very useful, as we will use in further sections.
4. Divisibility?
Let's think about Fibonacci numbers of the form 


If
,
. So trivially,
divides
. Does
divide
for all values of
?
Suppose this holds for some
. Now using the clever identity,
n}&space;=&space;F_{mn}F_{n+1}&space;+&space;F_{mn-1}F_n)
Since we assumed 

n})
&space;=&space;F_n)
Remember the first example 

&space;=&space;F_5&space;=&space;5)

5. General Case?
Now let's think about more general case when 




)
Again using our clever identity,

. Here we must observe two things.
is divisible by
(by result of previous section), so we can cancel out the term
when considering greatest common divisor
.
Next we should examine
. Denote this value as
. Since
, we have
, so that
)
But a common divisor of the successive Fibonacci numbers is 1 (since two are relatively prime), so that 
&space;=&space;\gcd(F_r,&space;F_m))
The Euclidean Algorithm ensures this repeated application of divisor algorithm ends in finite step, so that we can write a sequence of equations of the form

where each 
&space;&=&space;\gcd(F_r,&space;F_m)&space;\\&space;&=&space;\gcd(F_r,&space;F_{r_1})&space;\\&space;&=&space;\gcd(F_{r_1},&space;F_{r_2})&space;\\&space;&=&space;...&space;\\&space;&=&space;\gcd(F_{r_k},&space;F_{r_{k+1}})&space;\end{align*})
The last equation, 


=&space;F_{r_{k+1}})
where )
&space;=&space;F_{\gcd(n,m)})
Let's verify this final result using examples above.
Good!
6. Fibonacci Primes
Interestingly, the converse of results obtained from Section 4 can be derived using our ultimate relationship, &space;=&space;F_{\gcd(n,m)})
If 
&space;=&space;F_{\gcd(n,m)}&space;=&space;F_n)
&space;=&space;n&space;\implies&space;n\&space;|\&space;m)
So in the Fibonacci sequence, the following is true.
)
This brings up the question,
Above fact indicates that only possibilities are 


| p | F_p |
|---|---|
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 7 | 13 |
| 11 | 89 |
| 13 | 233 |
| 17 | 1,597 |
| 23 | 28,657 |
| 29 | 514,229 |
| 43 | 433,494,437 |
| 47 | 2,971,215,073 |
| 83 | 99,194,853,094,755,497 |
| 131 | 1,066,340,417,491,710,595,814,572,169 |
| 137 | 9,134,702,400,093,278,081,449,423,917 |
Fibonacci primes become rarer as the index increases. 




7. Conclusion
- Fibonacci sequence grows rapidly, with recurrence relation
)
Greatest common divisor of two fibonacci numbers
is equal to fibonacci number indexed by the greatest common divisor of two indices
.
The building blocks of Fibonacci sequence are Fibonacci primes which become rarer as the index increases.
P.S It is NOT known whether there are infinitely many Fibonacci primes... 😕
8. Citations
[1] By Jahobr [CC0], from Wikimedia Commons, Source Link
[2] List of Fibonacci Primes with factorization
Starting from this post, I promise not to use images in the Web without any proper copyright citations. Instead I will use my own drawings and diagrams for explanations. I apologize for any misuses of images related to my previous posts.


&space;=&space;3&space;=&space;F_4)
&space;=&space;F_{\gcd(8,&space;20)}&space;=&space;F_4)
&space;=&space;F_{\gcd(11,&space;21)}&space;=&space;F_1)
Nice post. For anyone curous about the largest fibonacci prime, the largest confirmed prime is F104911 and is a whopping 21925 digits long. Unconfirmed ones are even larger.
Congratulations @mathsolver! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Wow great explanation man,keep it up..
Congratulations @mathsolver! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOP