While Mathematics is one of the most viewed difficult subject in the curriculum, my post about Math aim to dispel the fear that students have on it.
As I love to write about Math, let me see how far I can go here in Steemit as I'm on my first post. I'll try to make it reader - friendly in the sense that the language used in the presentation of the lesson is easily understood.
The purpose of this post
The purpose of this post is to review the basic terms and concepts in algebra which are deemed important in understanding the succeeding topics. As we all know learning algebra is similar to learning language. It is therefore important to learn the most commonly used words and symbols in which one cannot solve problem by simply utilizing arithmetic. And today's post aimed one to develop an understanding of the set of real numbers.
Topic: Symbol of Algebra - Set of real numbers
One of the basic symbol of algebra includes numbers. The set of real numbers is the union of the set of rational numbers and the set of irrational numbers.
This implies that any rational or irrational number is a real number. They are termed real numbers because they represent real-world quantities.
Examples of rational number

are integers and b is not equal to zero (0). It can be expressed as decimal number may either be terminating or a repeating non-terminating decimal such as 2/3 or .666....You might be surprised to know that a repeating decimal is a rational number.A number that can be expressed in the form of (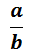 ); where
); where
Below shows examples of the different types of rational.
• 1/5 is a rational number (1 divided by 5, or the ratio of 1 to 5)
• 0.75 is a rational number (3/4)
• 1 is a rational number (1/1)
• 3 is a rational number (3/1)
• 85.5 is a rational number (513/6)
• −14.2 is a rational number (−213/15)
Examples of Irrational number
Decimals that are non-terminating and non repeating are called Irrational numbers. These numbers do not contain a subsequence of digits, the repetition of which makes up the tail of the representation. Their canonical form may be obtained by dividing a and b by their greatest common divisor, and, if b < 0, changing the sign of the resulting numerator and denominator.
Below shows examples of the different types of irrational.
•
• 𝝅 = 3.1416...
• e = 2.718...
Real life situation
Accoridng to Kimberlee Davison in one of his article, a mental trick you can use to help you visualize whether a number is rational or irrational is to think of the number in terms of cutting pizzas. For instance, if a number is rational, you can imagine cutting pizzas into equal-sized slices described by the denominator of a fraction and then eating the number of slices described by the numerator. For example, 6/8 can be found by cutting a pizza into 8 slices and then consuming 6 of those slices.
For a number like 3.95, you imagine cutting pizzas into a hundred slices each and then taking 395 slices. While you'll probably never be quite that hungry, you can imagine it. A negative number like -3/10 is a little tougher, but you could still visualize it if you slice pizzas into tenths and then give back 3 slices.
It's impossible to think of the square root of 5 that way. While there might be some other way to figure out how to get exactly the square root of 5 pizzas, you can't do it by cutting the pizza into any set number of equal slices and then taking the correct share of those.
In most cases, the best we can do to visualize an irrational number is approximate it with a decimal number.
References:
2.Textbook in Intermediate Algebra II
1.https://study.com/academy/lesson/what-are-irrational-numbers-definition-examples-quiz.html
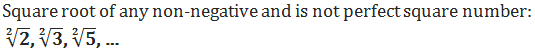
Congratulations @morikin! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
To support your work, I also upvoted your post!
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPMath is fun!!!
true...😅though often mindblowing..
thanks for dropping by openparadigm