Consider any real or complex variables q, and let's take a look at the expression
which can also be written as
Read this as a function in q, i.e. consider the following polynomial, which we'll call "u6"
This polynomial has an important property, namely that when you plug in q=1, you find the value 6:
Here is the graph of the function, u6(q), with q interpreted as real number in the inteveral from -1 and 2.
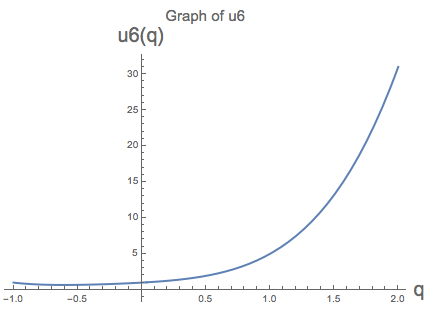
For sure, if you have any non-negative integer k, then q^k at q=1 equals 1^k, which is just 1. For this reason, any polynomial that is the sum n terms of the form q^k, will, at q=1, evaluate to n. For example, consider
If fulfulls
Now, more generally, let's consider a function u(n,q) of two arguments. The first argument shall be an integer, n, and the second any other number, q.
As I hope I've motivated above, this function fulfulls
This has a surprising consequence: The arithmetic of natural numbers is embedded in the arithmetic of those functions.
For example, consider the function u(2,q) and u(3,q). Define two new functions, f and s, like so:
and
which means
and
Because of what's been said before, those two functions are actually just deformations of the numbers five and six. Indeed
and
We see that we can abstract away from the natural numbers and works with functions, which secretly at one point know about basic arithmetic. However, at the pint q=3.5, the u's will not look related to the natural numbers and their arithmetic is something much wilder.
The most serious application of this concept is in combinatorics of vector spaces. The subject goes by the name of q-analogs and has toy applications in various fields.

You have your q-derivative and the q-integeration and there are literally infinitely other ways to extend the natural numbers in a similar way.

Another variation of this idea goes by the name quantum calculus. Other interesting applications are for deviant definitions of entropy.
In fact, I have some q-analogs that I came up with, one where q doesn't have to be from what is called a field in mathematics (something like the real or complex numbers), that I come back to every now and then.
Let me know if particular aspects of this in-between of algebra and analysis are of interest to you.
Take care
@qed
Cool! Learnt something new today. So this is basically a way of generalising known functions/theorems to more general cases?
Not only that, but yes.
For q in the complex numbers C, the neat thing that e.g. u(18,q) is the number 18, but you can apply analytic operations to it. For example, you can take the derivative d/dq of u(18,q) and you get some other creature.
The q-analog of some binomial coefficients (there are a few) have also hands-on interpretations in the combinatorics of particular spaces, where e.g q index the dimension.
Going further towads what I said at the end, you can use the principle even with a broader approach.
Consider any sort of space Q (such as the complex numbers, but also R^3, if you will) and let p be a point in Q. Let A be some sort of algebra in which division with a unit makes sense (such as the complex numbers). Consider now a sequence of functions Q->A i.e.
a : N -> (Q->A)
This
Define the deformation of a natural number n in N as
[n]_a(q,p) := sum over k from 0 to (n-1) of a_k(q) / a_k(p)
In the limit q to p, the quotients a_k(q) / a_k(p) become 1 and thus
[n]_a(p,p) = n
This is like the above situation, except before a_k(q)=q^k was a very simple function. There is no need to restrict outself to that, execpt that the above sum u(k,q) has a closed expression representation.
Thanks! My brother, @mckeown12 was trying to teach me this stuff, but I wasn't understanding it over the phone...
That's funny.
Yeah that made me laugh too!