In this post I will go over the general notion of a continuous function between two topological spaces. I will assume the reader is familiar with the idea of a topology on a set and open sets in the given topology which I covered in a previous post.
The idea of continuous functions is usually first encountered in a calculus course where a function f(x) is defined to be continuous at the point x = a if the limit as x approaches a of f(x) exists and is equal to f(a). This concept of continuity forms the basis for much of the subject of real analysis.
Notice that this definition depends on the concept of a limit which makes use of the distance or metric on the set of real numbers. However, there are many abstract spaces that mathematicians want to study that do not have a way of measuring the distance between points.
Thus we are led to make a more general notion of continuous function between two topological spaces that will agree with the limit definition given above when we take our spaces to be the set of real numbers with the usual Euclidean metric.
The proper way to do this might seem strange on first encounter but it also is simpler to define because we do not need to rely on any technical tools such as limits and the epsilon delta definition that this entails.
Definition:
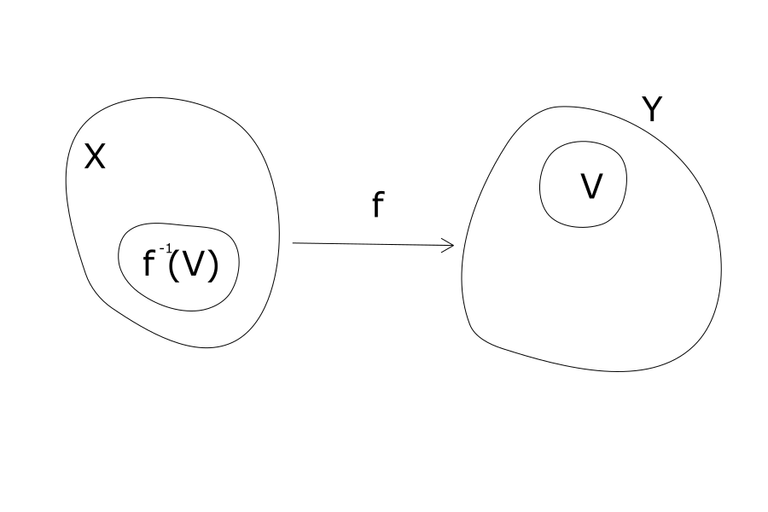
Suppose that f is a function from the topological space X in to the topological space Y. We will say that f is a continuous function if for each open subset V contained in Y then we have f-1(V) is an open subset of X.
Thus a continuous function is one for which the inverse image of any open set in the codomain is also an open subset of the domain of the function. Notice that if the domain X has the discrete topology in which every subset of X is open if follows that any function with domain of X in to any other topological space is continuous.
Furthermore, if Y has the indiscrete topology in which the only open sets are the empty set and Y then it follows from the definition that a function from any topological space X in to Y is continuous.
As another example consider the function from the interval [0, 1) to the unit circle given by f(x) = ei2πx. This defines a continuous function between these two topological spaces when thought of a subspaces of the real numbers and euclidean plane respectively.
It follows from the definition above that continuous functions can also be defined in terms of closed subsets. In fact, we can say that a function between two topological spaces is continuous if the inverse image of any closed subset of the codomain is a closed subset of the domain of the function. This alternative definition is sometimes easier to check depending on how the topology is defined on your spaces.
In this post we have discussed the idea of a continuous function between topological spaces. Continuous functions are of fundamental importance in the area of mathematics known as topology and I will discuss this further in later posts.
References:
https://en.wikipedia.org/wiki/Continuous_function#Continuous_functions_between_topological_spaces
http://mathworld.wolfram.com/ContinuousMap.html
Why do you call e^{2 \pi x} a unit circle? That would make sense if x was purely imaginary, but not on the [0,1) interval. Also, can you point me to a link that shows how math markup done in steemit?
Yes, it should have been ei2πx. I don't have a link for math markup. I am just using the sup tag from html and unicode character for π.
Interesting.
Yes, I had read continuity of function in calculus but it was extended to topological spaces. I haven't taken topology classes but now got some idea.
Remember learning this long ago,:) topology is an interesting topic, id read more!
Thanks