I've just read and upvoted Negative Exponents, an introduction. I was writing a comment to add my notes, until I realized that maybe a post could be fine. Maybe not. I don't know. Teaching is a hard thing and different explanations of the same topic could reach different people. Thus, here we go. I'm not saying something different, I'm just saying it differently, with another angle, so to speak.
Unfortunately, Steemit does NOT support math!
I want to show how you give meaning to b0 and b-n (being n a positive integer) — negative exponents — only taking into account notation. Notation is something conventional, yet it must be meaningful and consistent. In his previous post, Exponents, an introduction, @mathworksheets correctly wrote
In simple words, exponents are the shorter way to write the repeated multiplication of a number.
We don't need to know anything else to build the rest. Well, almost anything else: we must know what are +, ×… I hope readers know the very basic math.
Let's repeat that it's a notation to repeat multiplication…
It could be cut down in these steps.
- bn means (notation!) b×b×b×...×b (n occurrences of b),
- you can write it like this: (b×b×…×b, b appears k times) × (b×b×…×b, m times), with the number of b being always n, hence k+m = n (we've just grouped them);
- then you can write it as bkbm, and this must be by construction the same number of bn;
- so bkbm = bk+m = bn
We can generalize:
- if we have bN1bN2…bNn, we can write b∑iNi
The ∑iNi is just another notation, meaning that we must compute the sum (∑ is the summation symbol) N1 + N2 + N3 + … + Nn; this “expansion” is obtained by replacing i with 1 for the first addend, with 2 for the second addend, with 3 for the third addend… And so on, until we reach our maximum value, n, which here is implicit: ∑i means that i is the index we're going to replace and increment, but it doesn't specify the starting value — we assume it must be 1 — and the last value — we assume it must be n. It is a short form of the more complete ∑i=1n, which looks ugly because of lack of support for math (I'm just using characters and sup and sub tag, not meant to be used to typeset subscript and superscript in a math context).
It's important to remember that this is a chosen notation
- bn means b×b×b×…×b (b repeated n times)
but the following is a conseguence of the above one:
- bi·bj·bk = bi+j+k
(Usually the multiplication symbol is omitted, so that abc means a×b×c, and indeed usually the multiplication symbol is · — a dot in the middle, which I've used above — instead of ×… But if we agree on the meaning, it doesn't matter which symbols I use.)
What does b-n could possibly mean?
Let's start with what we already know:
- bn·bm = bn+m
It is what we've already seen when n and m are positive, non-zero integer numbers. What if n=-3 and m=4? We have this
- b-3·b4 = b1
Important: we have applied mechanically the “sum of the exponents” rule which we have deduced after we have chosen the meaning of the notation. Expanded (so to say)
- b-3·b·b·b·b = b
- i.e. (a mysterious number)·b·b·b·b = b
Now our task is to deduce a meaning for b-3 — it's a number, and replacing that expression with that number (even if unknown, because we don't know b, after all), the equation must hold true. As said above, it's notation, but it must be consistent…
Moreover, it's better if we play according to the razor of Occam. So, which is the number that multiplied by b·b·b·b gives b? Thanks to basic math, we know that it must be this:
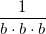
(LaTeX notation: \frac{1}{b\cdot b\cdot b})
Well, three b, and we had b-3… We can test with other numbers, we'll land on the same conclusion. Hence
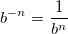
(LaTeX notation: b^{-n} = \frac{1}{b^n})
So we deduce another rule: if you have b-n, you can turn it into a fraction changing the exponent sign, namely 1/b-(-n). And we know that -(-n) is n, doesn't we? It means that you can also do this: bn = 1/b-n.
Again, I want to stress that we've chosen a notation (the meaning of bn as n-times repeated multiplication of b, when n is a positive non-zero integer), and we are deducing the rest to keep the notation meaningful and consistent (with itself and the rest of the mathematics).
What does b0 mean then?
This is straightforward.
- b0 = b-1+1 = b-1·b1 = b/b
This is why we say that b0 = 1. Then you can think about the meaning of it when b = 0…
What about fractional exponents?
In stead of integer numbers, we could use rational numbers. To understand how we can cope with them, given all that we've seen so far, we need to show that (bn)m = bn·m is consistent with the meaning of our notation.
- let p = bn = b×b×b×…×b, b repeated n times (by definition)
- pm = p×p×…×p, p repeated m times (by definition)
Now, what do we have if we “expand” each p in the second line? (By expanding I mean that we replace each p with its definition given in the first line). I want to show you the “grouping”, so be patient with the poor textual graphics.
___________
/ \ b repeated n times
b × b × … × b
\__,________/
/
/ p by definition is b repeated n times
|
p × p × p × … × p
\_______________/
p repeated m times
Once we've replaced a single p, we'll count n bs. When we replace the second p, we'll count other n bs, i.e. b will appear n+n times, i.e. 2n times — and we've replaced two p only. We continue replacing the third p, then b will appear 3n times; we have m ps, so when we have replaced all those ps, we'll count m·n bs.
If we use our short notation,
- pm = p·pm-1 = bn·pm-1
- bn·pm-1 = bn·bn·pm-2
And so on, until we have what we expect, i.e. bn repeated m times, and we know we can sum the exponents: n + n + … + n, n repeated m times, and we'll use the notation for the multiplication (m·n), so we write bm·n.
We've shown what we need: take pm and replace p with its definition, bn: (bn)m. This must be bn·m (or bm·n, of course), because of the above.
Now we reason in a way similar to what we've done for b-n, but instead of sums of exponents, we have multiplication of exponents.
Consider this:
- (b1/n)n
We want to give a meaning (a consistent meaning, a meaning that plays well with all the already deduced rules) to the number inside the parenthesis. By the rules we've once again deduced starting from the definition of our notation bn, we know that it must be equal to bn/n, which is simply b.
Now, which is that number that, when multiplicated with itself n times, gives b? The answer to this question is part of the definition of the root operation!
Let's suppose n=2. Which is that number that, when multiplied by itself, gives b? It's √b. Another notation, by the way! And we know that √b·√b = b. So here it is that number. (Computing it once we assigned an actual number to b is a totally different story.)
Thus, with our “exponential notation”, (b1/2)2 = (by definition…) b1/2·b1/2 which is, applying the rule, b1/2 + 1/2 = b1 = b.
The same we can see with different values for n.
We can easily give meaning to b3/2, and everything else… This example is: (b3)1/2 = √(b3).
One notation to rule them all
If you have a fraction with a very long expression in the denominator, you could replace a long fraction-line with this:
- (this is a very long and complicated expression)-1
If you have a long and complicated expression you must compute the cube-root of, you can write:
- (a long and complicated expression)1/3
If you spot errors, drop a line as comment. If you haven't understood a thing, likely you are among those who prefer another approach to the same topic — then the article linked at the beginning, and its follow-ups, could be better for you. If you think some parts are too obscure and have suggestions to make them simpler, drop a line, again — or “fork” writing your own way! “Distributed”, linked efforts to make explanations of math things easier and better for everyone could be interesting.
It wasn't me for me, but I like your explanation. Also, you made me want to learn latex.
LaTeX is very useful, and it isn't that hard, at least for the common usage.