Sets
Today, I'm going to talk about one of the most monumental result in set theory-- that some infinities are larger than some infinities. This statement is ambiguous of course, in what sense are we comparing infinities exactly? In this post, what we are going to compare are sets, infinite sets, to be exact. But what are sets? To make things simple, we say that a set is just a collection of distinct objects. Sets can be a collection of anything, really, so let's say that Swikipedia page for it. For this post, we'll talk about well-defined sets-- sets in which we know whenever any object is a member of it or not. is the set of all elephants, in the set-builder notation, we can write it as 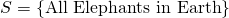 . So we can just think of infinite sets as sets with infinite number of objects in it. There are some intricate details about sets, and actually we can define 'sets' which are not consistent; for examples of non consistent or paradoxical sets, there's a good
. So we can just think of infinite sets as sets with infinite number of objects in it. There are some intricate details about sets, and actually we can define 'sets' which are not consistent; for examples of non consistent or paradoxical sets, there's a good
The Natural numbers and Real numbers
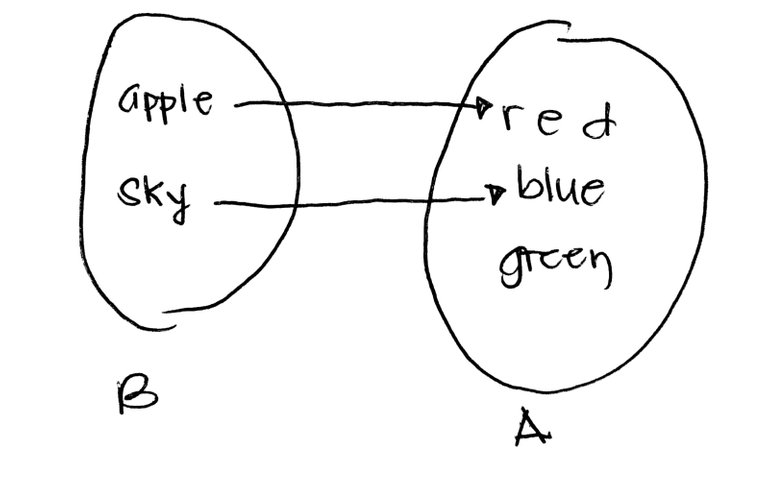
Before we go on, we'll first need some infinite sets to work on. For this post, we'll work primarily with the set of nonnegative whole numbers (or natural numbers)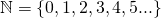 and the set of real numbers which we'll denote by
and the set of real numbers which we'll denote by 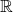 . Now, the theory of real numbers themselves is quite deep, but I will only describe this set in an intuitive way for this post. There are several way of seeing real numbers, but I think the simplest one is the perspective that real numbers correspond to each point in an infinitely long line like in the image below:
. Now, the theory of real numbers themselves is quite deep, but I will only describe this set in an intuitive way for this post. There are several way of seeing real numbers, but I think the simplest one is the perspective that real numbers correspond to each point in an infinitely long line like in the image below:
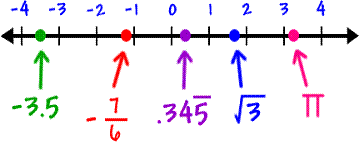
The set of real numbers is comprised of the union of irrational and rational numbers. The rational numbers, which are just the fractions like 1/23.14. contains the integers, which are the the positive and negative whole numbers, along with zero. The integers, in turn, contain the natural numbers. The irrational numbers are, on the other hand, a lot more complicated (they probably deserve a post of their own), but their discovery is what led to the definition of real numbers; they can be thought of as the numbers which cannot be written as a fraction. If we write them in their decimal form, they'll appear as numbers which has an infinitely many digits after their 'decimal point', an example is the number pi 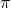 , which we usually approximate as
, which we usually approximate as
Comparing Sets
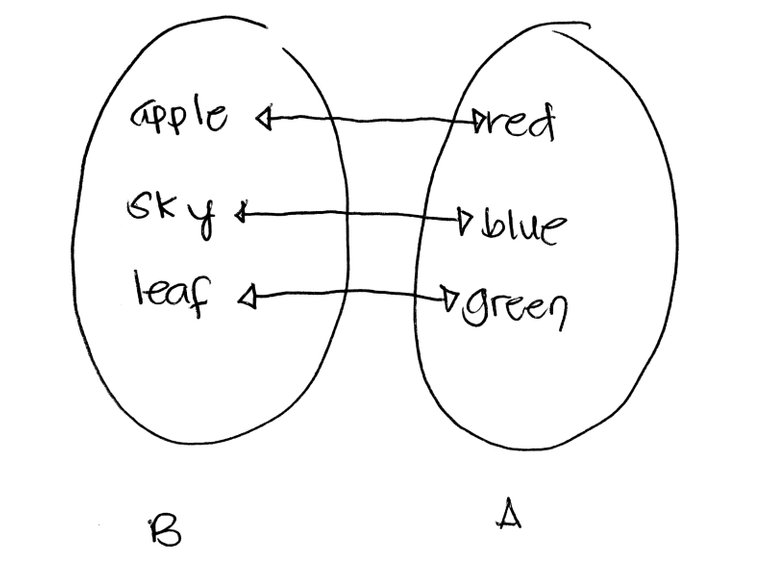
3 elements in it, while the second one only has 2cardinality, since they both have the same number of elements, namely, 3. Seems pretty easy and straightforward right? You just have to count the individual elements of each set after all. Not really, we actually have to refine our technique of comparing sets, it will be apparent later why, but for now let's take a different approach. Let's say we have two sets A and B, and say that A has a cardinality that is greater than or equal to B when for each member or element of B, we can assign to it a distinct member of AA larger than B, we'll show that this method works just the same: we can assign apple from B to red in A, and sky in B to blue in A as summarized by the illustration belowSo how exactly do we compare sets? Let's do a very simple example first, consider these two sets: 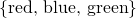 and
and 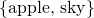 , the first set is obviously larger than the second set since it has elements in it. Now, consider a slightly different pair of sets:
, the first set is obviously larger than the second set since it has elements in it. Now, consider a slightly different pair of sets: 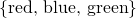 and
and  , it's pretty easy to see that they have the same 'size', or in more technical terms, they have the same , we denote it by
, it's pretty easy to see that they have the same 'size', or in more technical terms, they have the same , we denote it by 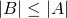 . To illustrate, let's take
. To illustrate, let's take 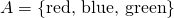 and
and  as before. We already know from out previous technique that the cardinality of
as before. We already know from out previous technique that the cardinality of
Since we have assigned every member of B to a distinct member of A, then by our definition, A has a larger cardinality than B. Note that it actually doesn't matter how we assign each element above, we can assign apple to green and sky to redeach, I mean ALL) member of A to distinct members of B, one of them will always be left out . From now on, this is how we'll be comparing sets., it actually doesn't matter-- what matters is that a one-to-one assignment exists. Also, for the example above, we actually have a strict inequality, that is, 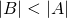 since we cannot have that
since we cannot have that 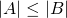 , this is because we cannot find any reverse assignment of each (by
, this is because we cannot find any reverse assignment of each (by
So what about when A and B have the same cardinality? This is, in a way, easier to understand; A and B have the same cardinality when we can pair off each distinct member of them, we denote this by 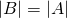 . To illustrate, let us again use the example above, let's take
. To illustrate, let us again use the example above, let's take 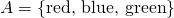 and
and 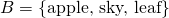 , we immediately see that we can pair off each member like so:
, we immediately see that we can pair off each member like so:
Again, it doesn't really matter how we pair off each member, what is important is that such pairings exist between sets. Also, observe that 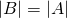 is equivalent to
is equivalent to  and
and 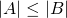
Comparing Infinite Sets
So why do we have to do all that just to compare sets when we can just count their elements? You might have already thought of it mid-way, but we can't do that with infinite sets like the set of natural numbers 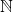 and real numbers
and real numbers 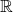 . If you start counting any of them, you'll never get to the end of it.
. If you start counting any of them, you'll never get to the end of it.

The technique that we used above has the advantage of being able to compare both infinite and finite sets.
The Diagonalization Argument
nless than or equal the cardinality of the real numbers. This result isn't very satisfying since it tells us something that we already know about, that the naturals are embedded to the reals. Since our last result says "less than or equaldistinctdistinctall of the real numbers as if they are like natural numbers like so:We can now begin comparing the two infinite sets, 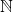 and
and 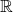 . As I have said before, the set of all real numbers
. As I have said before, the set of all real numbers 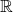 contains the set of all natural numbers
contains the set of all natural numbers 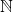 . Therefore, it is pretty easy to see that
. Therefore, it is pretty easy to see that  , since we can just assign each natural number to themselves in
, since we can just assign each natural number to themselves in 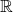 . Again,
. Again,  means that the natural numbers have a cardinality that is ", we'd want to sharpen our comparison between these two infinite sets, is the comparison strict, that is,
means that the natural numbers have a cardinality that is ", we'd want to sharpen our comparison between these two infinite sets, is the comparison strict, that is, 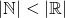 ? Or are they "equally dense" as sets, that is,
? Or are they "equally dense" as sets, that is,  ? Only one of these two is correct, but let us assume that
? Only one of these two is correct, but let us assume that  and see what happens. If
and see what happens. If  , then we can pair each real number in
, then we can pair each real number in 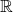 to each natural number in
to each natural number in 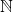 ; this is tantamount to saying that we can arbitrarily list
; this is tantamount to saying that we can arbitrarily list
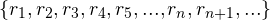
It might get a little confusing from this point on, since book-keeping on both the notations and the digits that will appear might get too cumbersome, but I honestly believe that this is one of the cleverest trick that I have seen in mathematics, so just try to hang on.
0's and 1's. Since we assumed that all the real numbers can be listed like the one above, we can as well list this subset like natural numbers. So just for demonstration let us give some values to the list of real numbers above:We can make an arbitrary assignment to the real numbers above, so for simplicity, we are going to consider a subset of the real numbers with forms like  , that is, real numbers in decimal form (remember that a real number can have an infinite number of digits to its decimal form), where their whole number part is zero, and the digits after the zero are just made up of
, that is, real numbers in decimal form (remember that a real number can have an infinite number of digits to its decimal form), where their whole number part is zero, and the digits after the zero are just made up of

1, we 'flip' it to 0, and this 00, so we 'flip' it to 1n'thn'th0j2ndj, because they have different jThese are just some of the values for the set of reals that we have above, but this should suffice for demonstration. Let us now construct another real number  using the digits after the decimal point. The form of our new real number will have a whole number part 0, and its first digit after the decimal point will depend on the first digit after the decimal point of
using the digits after the decimal point. The form of our new real number will have a whole number part 0, and its first digit after the decimal point will depend on the first digit after the decimal point of 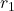 , which is will become the first digit after the decimal of our new real number, so we have
, which is will become the first digit after the decimal of our new real number, so we have  . From hereon, we refer to 'digits' as digits after the decimal point. So to get the next digit of our new number
. From hereon, we refer to 'digits' as digits after the decimal point. So to get the next digit of our new number  , we look at the second digit of
, we look at the second digit of 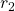 , we see that it is , and make it the second digit of our new number, therefore
, we see that it is , and make it the second digit of our new number, therefore 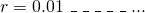 . You may now see where this argument is going, and this is the reason why I highlighted the 'diagonal' digits of the first six real numbers in our list. In general, the digit of
. You may now see where this argument is going, and this is the reason why I highlighted the 'diagonal' digits of the first six real numbers in our list. In general, the digit of  is the 'flipped' value of the digit of
is the 'flipped' value of the digit of 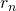 . So, looking at the highlighted digits above, the first six digits of
. So, looking at the highlighted digits above, the first six digits of  is
is 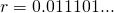 . The real number
. The real number  has the same form as in the list that we consider-- it has a whole number value of with binary digits after the decimal point, so it must occur, by hypothesis in the list
has the same form as in the list that we consider-- it has a whole number value of with binary digits after the decimal point, so it must occur, by hypothesis in the list  . So it must be that
. So it must be that 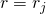 where is some whole number. Let's check, is
where is some whole number. Let's check, is 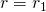 ? No, because the first digit of
? No, because the first digit of  is 0, while the first digit of
is 0, while the first digit of 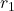 is 1. Similarly, it can't be
is 1. Similarly, it can't be 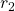 because they do not have the same digit. In general,
because they do not have the same digit. In general, 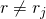 for any natural number 'th element by construction. Thus we have a contradiction, since
for any natural number 'th element by construction. Thus we have a contradiction, since  is simultaneously both in and not in the list. The method that we used is called the diagonalization argument.
is simultaneously both in and not in the list. The method that we used is called the diagonalization argument.
Quoting Arthur Conan Doyle "Once you eliminate the impossible, whatever remains, no matter how improbable, must be the truth". Since we have eliminated the case: 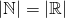 , then the only remaining case
, then the only remaining case 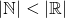 must be the truth.
must be the truth.
Its Implications
1, we know immediately that 2 is the next whole number, but this is not the case for real numbers. If you start from 1, you do not know what really the 'next' real number is, because they are so 'densely packed' together that there is always another real number between two different real number. To demonstrate, there is always 1/2 between 1 and 2, and between 1 and 1/2, there is 1/4; worse, there's some pi between your 3 and 3.2Continuum Hypothesis. Although years later, after refining our foundations of mathematical logic, it was shown to be unprovable-- at least in a sufficiently reasonable set of axioms of set theory, the Continuum Hypothesis turned out to be a statement that can be true and false at the same time. This result came later after the original mathematician who posed the Continuum hypothesis passed away.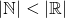 means that we can never list the real numbers like we count numbers. For example, when we count from . There are also some theoretical implications on the non equality of the cardinality of naturals and reals. Since
means that we can never list the real numbers like we count numbers. For example, when we count from . There are also some theoretical implications on the non equality of the cardinality of naturals and reals. Since 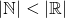 , does there exist a set
, does there exist a set 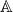 such that its cardinality is in between
such that its cardinality is in between 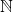 and
and 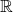 , that is,
, that is, 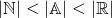 ? As originally posed, it was believed that no such set exists, this conjecture was them known as the
? As originally posed, it was believed that no such set exists, this conjecture was them known as the
Georg Cantor
I refrained from referencing him because I wanted to dedicate a whole section to him. All of the results above, we owe to Georg Cantor's genius. He was the one who pioneered the study of Set Theory in its own right, thereby making a huge impact on the foundations of mathematics-- since then mathematical theories were translated into the language of Set Theory. Some mathematicians hailed him, one of them was David Hilbert, who likened his works to paradise, as he made the study of mathematics clearer for everyone. But in his lifetime he was also ostracized by his contemporaries, one of them being his past mentor as his results clashed with his teacher's school of thought. For the remaining years of his life, he was plagued by chronic mental illness including depression-- being criticized by other mathematicians, and not being able to prove the Continuum Hypothesis, which was the brainchild of his Magnum Opus-- the Diagonalization Argument, not knowing that his time still lacks the necessary logical foundation to tackle the problem. He eventually succumbed to a heart attack, dying away from his family in a sanatorium.
Note:
For this post, I just cross checked their respective wikipedia pages, especially on Georg Cantor. For the diagonalization proof, I referenced my old undergrad notes.
This post became longer than I had intended, so it's a lot harder to proofread now. Please let me know if there are any blatant errors above.
I think that using the examples that you use it makes more sense to talk about countable versus uncountable in this setting. Countable has meaning in a finite and in a single infinite setting while for uncountable there are many different infinite settings.
Also note that by defnition a question cannot be a hypothesis. The continuum hypothesis is there is no set between the cardinality of the natural numbers and the reals.
What do you mean different infinite settings? Do you mean climbing up the 'infinity' ladder by taking power sets of infinite sets? Anyway, I was reluctant on using countables and uncountables because I didn't want to keep introducing new concepts.
Yeah, you're correct about CH, that's embarrassing, I edited the article accordingly. Thank you.
I agree that discussing the general concept of infinity (by which I mean ordinals) is unnecessary for an introduction. I meant to say that if you are only discussing countable and uncountable then you can directly start with this as opposed to starting with infinity which is much broader concept. But this is a matter of taste I think.
Hmm, I guess you're right. It might have been better to center this whole article about countability and uncountability, but obviously, at some point, I got carried away with injections and bijections that I kind of lost the chance to introduce it, I was rushing to get to diagonalization, I really like it lol. This isn't exactly friendly to non-mathematicians I guess.
Congratulations @blackiris! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP