I am a mathematics graduate student from the Philippines, and I figured out that this site is a good platform to dump my thoughts about mathematics (and possibly other geeky stuff). What I'm planning here is pretty much to regularly write about what I currently know about mathematics while trying to explain it to the general lay audience.
So what exactly do these math people do in particular, and why do some people bother to dedicate their lives to it? You might think we've already mapped out pretty much all of mathematics right? I mean, what could we possibly need to know more about numbers? Well, for starters, mathematics spans more than the concept of numbers. Some people actually refer to mathematics as the "formal study of patterns", and while patterns are predominant in numbers, we certainly do not only see patterns in numbers. Furthermore, we currently do not know everything about numbers. But just to demonstrate, let us first look at something that we do know about numbers, thus we'll define what a prime number is: it is simply any positive whole number p greater than 1 that cannot be divided by any other positive number except for itself and the number 1. For example, 7 is a prime number because it cannot be divided evenly by 2, 3, 4, 5, or 6, and it is divisible by itself, because 7 divided by 7 is just 1, and it is divisible by 1 because 7 divided by 1 is just 7. Similarly, 11, 13, 17 are primes. So we have a good idea of what primes are, and we will now state an important result about them: "for every positive number greater than 1, we can find a prime number that divides it". So for example, 6 can be divided by the prime 3 because 6/3=2, and similarly 25 is divisible by prime 5 since 25/5=5. We will use this fact, to prove that there are "infinitely many primes". To prove this, we are going to use a technique that is pretty well known among mathematicians, it's called "proof by contradiction", that is, we assume that something we are proving is false-- in our case, that there are only finitely many primes, and we should find a contradiction if we follow along this line of reasoning. So, if we assume that there are only finitely many primes, then we should be able to list it like so:

Pall our primes plus 1. Now, this is the important part of the trick, we can always write 1 as where
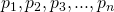 are all the prime numbers that you can find. Now, we make another number using these primes, let's call it , and define it like so:
are all the prime numbers that you can find. Now, we make another number using these primes, let's call it , and define it like so: 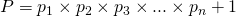 which is the product of
which is the product of
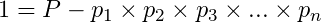
We use our previous result, that all positive numbers greater than 1 can be divided by some prime, and since, we assumed that all our prime is contained in the list above, then PPP11 cannot be divisible by any prime number, because every prime number is greater than 1, therefore we have a contradiction, hence prime numbers cannot be listed finitely. must be divisible by one of the 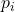 's in the list, and without loss of generality we can just assume that is divisible by
's in the list, and without loss of generality we can just assume that is divisible by 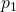 . Because is divisible by
. Because is divisible by 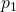 and
and 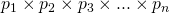 is also divisible by
is also divisible by 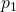 , then , as the difference of two numbers which are divisible by
, then , as the difference of two numbers which are divisible by 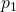 , must also be divisible by the prime
, must also be divisible by the prime 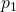 . But
. But
There you have it, that little piece of art above is what we call a proof, a bunch of statements stringed together by logic to arrive at a conclusion. If you made it until this point, I think you'll see that there is some exquisite beauty in proofs, that there is something elating about understanding a mathematical proof. Also, as a matter of fact, the proof above is pretty much the same proof that Euclid has shown thousands of years ago-- proofs transcend time, once found, they will always remain true for all eternity. This is what mathematicians really do, proving facts about mathematics-- not crunching really big numbers (some of them do that, but definitely not all), as some might think. Hence we go back to our first question, and I can say with confidence that this is the reason why some people are so hooked at math, it's just damn pretty.
Enough of my rambling, I hope you find my first post educational, and that you'll have a newfound appreciation of maths after this.
It's so beautiful to have you here on steemit. I took time to come welcome you and I know you will love it here. Welcome to our family. @greatness96
Hey thanks, this seems like a pretty cool community.
Welcome to Steemit! I'm also a mathematician. I think you'll agree we need LaTeX typesetting (Mathjax, or something like Overleaf) ... but things will get there as we get more science community users, I think.
I recommend the . It gives an alternative to having your posts be more widely seen while you still have little steem power.
It'd be really nice if the site can support LaTeX, it was quite hard to do all of that typesetting without it-- took me a lot of time and it still doesn't look good.
That was really cool, @blackiris! I'm an applied physics graduate myself, but all this math seriously drive me nuts sometimes. So salute yo you, Pinoy mathematician! That was an awesome write-up as well, so keep it up! 😊
Also, welcome to Steemit! Happy steeming! 🎉
Thanks, my undergraduate degree was actually in physics, I left it for pure maths because I liked proofs more than spidery computations and number crunching.
Welcome to the Steem World!
I have recently made an orientation video that will help you in your journey here - and will hopefully answer all the questions that took me months to figure out.
I wish you all the best here on Steem! https://steemit.com/dtube/@maneki-neko/rlfwsqlj
I will also use the tag : @originalworks for this post, this will summon a robot that, if you wrote this original article, will give you an additional upvote. :)
Welcome to steemit, @blackiris! ☺
thanks :)
Very cool post. Looking foward to more...math is the universal language.
New for my welcome speech...
Hey! Welcome to Steemit! This community is amazing but does take some getting use to since it’s a bit different than the other social media platforms.
I joined Steemit December 30th, 2017 and have had a blast networking, learning and earning (actually made some pretty good money so far)!
I'd suggest signing up for these free applications for Steemit that gets you upvotes and followers. The first thing you need to do as a new user is to increase your STEEM POWER (SP), which increases your visibility and voting power. These were a huge help for me.
Feel free to follow me @entrepreneur916, as I continue to post content to help make the Steemit community better and to help new members!
Respectfully yours,
Jacob A. Billett, M.B.A
CEO Billett Enterprises, Inc.
Hi @blackiris, first of all, Welcome to Steemit. I'm also new to this platform, I just started writing also. I just want to say, it's great to be here, I'm learning a lot, and here you are sharing your thoughts about Math, that's a great thing, not necessarily for me ~ not really fan of numbers. However, with the way you present it, I might like it someday. I like your writing style, keep it up. :-)
Well, I think people just generally have a bad experience with numbers during their younger years, perhaps due to a bad teacher, but I think most people can appreciate maths.
Hi
Welcome to Steem. It's an awesome community. I followed you. Please follow back. Good Luck.
Welcome! Math phd-student here. Will be following you :)
Note that for every positive number greater than 1, we can find a prime number that divides it is part of the fundamental theorem of arithmetic which also requires a proof. Idea for a second post?
It's part of FToA, without the uniqueness of the factors. This piece is quite hard to write since I kind of had to hand-wave that part here. I did went on without explaining why prime divisors always exist, so maybe, just for completion I'd talk about FToA in my next post. Thanks.
wow... amazing. continue working numbers which we hardly do.
Welcome to steemit. More Math tidbits in the future!☺
Hey thanks, that's what I'm planning.
welcome to steemit .. thanks for imparting your knowledge about mathematics . hope you will post more :)
@originalworks