Hi there. This post is on basic Set Theory in mathematics. This type of mathematics is different than the usual numbers and finding x.
When it comes to (abstract) topics such as Set Theory it is based more on relations and how things work and not so much on numbers and algebra.
A set is a collection of objects. These objects can include words, symbols or numbers. Examples can include:
- {shoe, sock, shirt, tie, pants}
- {1, 3, 5, 7, 9}
- {a, d, g, k, l, z, p}
(Note: I will be working with two sets.)
Sections
- Unions
- Intersections
- The Universe Of Discourse (U)
- Complements
- Subtracting Sets and Relative Complements
- Symmetric Difference
Unions
Given two sets A and B, the union of sets A and B are elements/items which belong to both A and B.
For two sets the shaded region represents the elements inside the union A ∪ B (A union B).
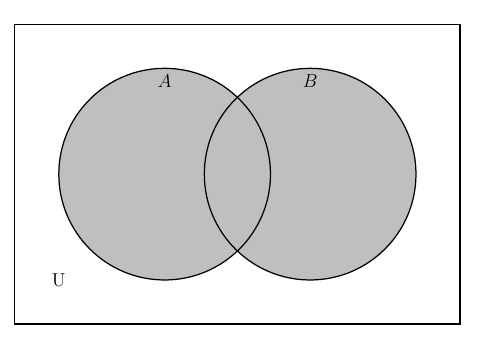
Example
Suposse two friends J and K meet each other to play video games. Each of them have their set of video games available to play.
| Friend J | Friend K |
|---|---|
| Mario Kart 8 | Super Mario 3D World |
| Yoshi's Wooly World | Donkey Kong Country: Tropical Freeze |
| Super Mario Maker | Mario Kart 8 |
| Pokken Tournament | Super Mario Maker |
What are the available video game choices?
Answer
For this problem, the union is used. The two friends can play from:
- Mario Kart 8
- Yoshi's Wooly World
- Super Mario Maker
- Super Mario 3D World
- Donkey Kong Country: Tropical Freeze
- Pokken Tournament
(Duplicates are excluded.)
In set notation, it would look like:
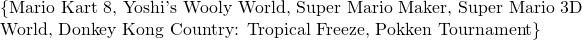
Intersections
The intersection of set A and set B denoted as A ∩ B (read A intersect B) is what is common between the two sets.
With the two sets, the intersection A ∩ B is represented by the shaded area in the visual below.
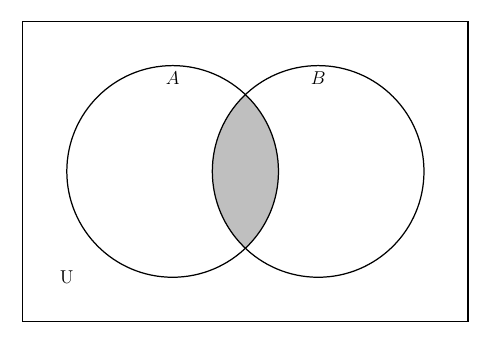
One can notice that the intersection A ∩ B is a subset of set A (A ∩ B ⊆ A) and A ∩ B is a subset of set B (A ∩ B ⊆ B). Items in the intersection belong to A and belong to B.
Empty Intersection
There are cases where there is nothing common between the two sets A and B. In this case, we say that the intersection A ∩ B is empty or disjoint. The intersection of such disjointed sets is denoted by A ∩ B = ∅ (where ∅ represents the empty set).
The visual below shows the shaded A region and the shaded B region but the middle intersection being unshaded representing an empty intersection. This is the union of sets A and B with an empty intersection.
Example One
What is common between the two classes with their favourite colours?
| Class A Favourite Colours | Class B Favourite Colours |
|---|---|
| Red | Pink |
| Green | Orange |
| Blue | Brown |
| Yellow | Green |
| Coral | Red |
| Grey | Black |
The intersection would be {Red, Green}.
Example Two
The intersection of the even numbers and the odd numbers is empty. No (whole and non-zero) number can be even and odd at the same time.
The Universe Of Discourse (U)
(Reference: https://www.quora.com/What-are-some-ways-of-thinking-about-a-universe-of-discourse-in-set-theory)
The universe of discourse is a large set which contain the items/elements of interest for the situation/problem. (There are more technical and abstract definitions for this but for this post I keep it simple.)
For this post, examples of the universe of discourse sets include:
- Students In A Classroom
- The Set Of Languages
- Computer Brands
- Fruits
There is no set larger than the universe of discourse. This concept will be made more clear in the next section.
Complements
In English, the word complement relates to an item that goes well with another item. In the mathematical set theory context, a complement refers to an opposite.
In the visual below, we have A' (or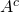 
) which is everything that is not in set A within the universe of discourse.
Notice how the intersection A ∩ B is not shaded. It is because the intersection belongs to A, so the intersection is not included in the complement of set A.
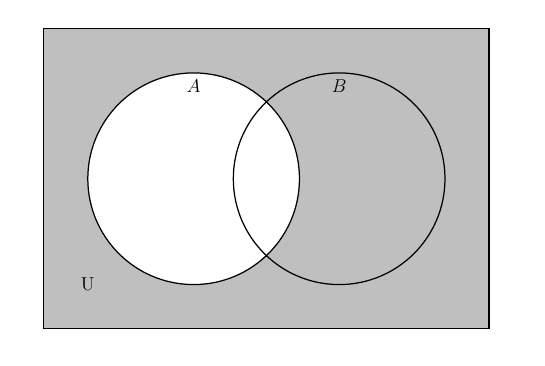
In this visual, we have B' (or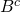 
). This means everything not in set B but within the universe of discourse (U). The intersection is a subset of set B it is not shaded.
This third visual is the complement of the union A ∪ B.
Example One
Given the numbers from 1 to 10 (inclusive) as the universe of discourse (U), the complement of even numbers from 1 to 10 are the odd numbers 1, 3, 5, 7 and 9.
**Example Two **
The universe of discourse set for this problem is a grocery list:
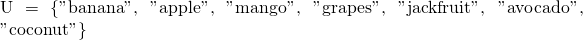
I have only one mango, one coconut, grapes and an apple. What am I missing?
Answer
The items missing are one banana, one avocado and one jackfruit.
Subtracting Sets and Relative Complements
There is subtraction with sets but it does not operate like 5 - 2 = 3.
In set notation (A - B) is the same as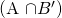 
. This means take all the elements in A that are not in B.
Symmetric Difference
The symmetric difference of the sets A and B is denoted by A Δ B. It is the elements from the union of the two sets which does not include the intersection.
In set notation, you have A Δ B = (A ∪ B) - (A ∩ B).
Example
Suppose we have sets A = {b, c, d, f} and B = {p, c, q}. The symmetric difference of sets A and B is:
A Δ B = {b, c, d, f} Δ {p, c, q} = {b, d, f, p, q}
The letter c is removed as it was common between sets A and B.
Notes
Set Theory is a part of (math) logic and it is useful for computer science people and computer programmers. One useful inforgraphic/image is from this link for SQL joins.
This type of math is interesting in the sense that it is more about understanding, logic and problem solving versus repetitive (and trial and error) from algebra.
This lesson can be taught to children (age 10+ I think) with the use of circles, and hula hoops. It is best to teach the children up to complements. This post was influenced by this Youtube video
This is a condensed and simpler version of this post from my website.
The Venn diagram images are from my LaTeX code in MikiTeX along with the Windows 10 Snipping Tool.
Just discovered your profile. A non-quant interested in learning more about stats/math so definitely looking forward to your posts!
Ah, welcome.
I see you have an interest in finance. I might touch on finance with math in my later posts. For now I am focused on math, and (stats) programming in R.