Hi. This is part one of two of working with square numbers and square roots.
Square Numbers
Recall that a square has four sides with the side lengths being all the same. Let s be the side length of the square. The formula for the area of a square is:
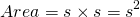
This area of a square is a square number.
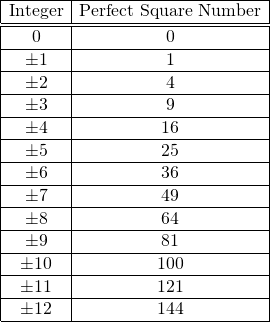
In this section, we deal with perfect square numbers where we have the side length s starting at 1 and then going up by one. That is we have the side length as +1, +2, and so on. (You could argue about the case for a side length of 0.)
The area of a square with each side length as 1 is 1 x 1 = 1 square unit. For a square of side length 2, the area would be 2 x 2 = 4 square units. With a side length of 3, the associated perfect square number would be 3 x 3 = 9. The table below continues to 12 for the side length of a square.
| Side Length Of Square (s) | Square Number (Area = s x s) |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
| 11 | 121 |
| 12 | 144 |
Square Roots
In the previous section, we find the area of a square with a known side length of a square. With the square root, we go in the reverse direction. That is, the side length of a square can be determined if we know the area of a square.
If the area of a square is 100 square units, the side length of the square is 10 units. This 10 is the square root of 100. Another example would be the square root of 64 is 8 since 8 x 8 = 64. You could ask yourself, "Given a square number what number multiplied by itself gives me this square number?"
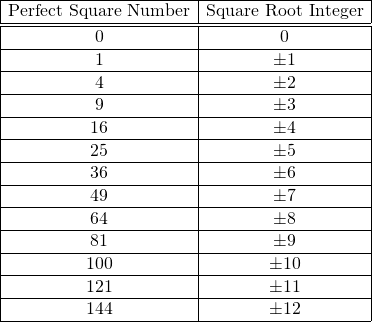
Here is the table of square roots and their associated square roots. It is similar to the table presented above but the columns are switched. Perfect square numbers are used here. You could include the 0 case where the square root of 0 is 0. Note that the side lengths here are positive.
(Note: It is not possible to take the square root of a negative number in the real numbers system.)
| Square Number (Area = s x s) | Side Length Of Square |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
| 121 | 11 |
| 144 | 12 |
Considering Negative Numbers
In the previous two sections, we have dealt with positive whole numbers (integers). The concept of square unit lengths and areas were used as a way to help with understanding. The negative numbers are now considered.
The square root of a positive number can be negative. As an example, the square root of 25 is both +5 and - 5 since 5 x 5 = 25 and (-5) x (-5) = +25. A negative multiplied by another negative is a positive. In math notation the square root of 25 can be shown like this.
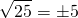
This plus/minus sign means it could be only one of +5 or -5.
The table from the first section can be revised to this.
The table from the second section can be updated to the one below.
Note: The number inside the square root has to be non-negative but the answer resulting from the square root can be negative. In math notation, you would have:
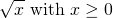
Edit: Included a generic square picture.