The factorial number is present in most combinations problems, so it is important that we handle this tool in different situations. Therefore, we will study the ways to handle factorial numbers algebraically to solve equations.
The factorial of a number is the successive multiplication of the number with all its natural predecessors. So when you have an equation in which the unknown accompanies a factor, the way to obtain the solution is we can simplify this factor or rewrite the equation so that the factor does not interfere or is in a way that allows us to use some mathematical tool for solving equations, whether they are first or second degree.
We will see examples that permeate the algebraic manipulations with the factorial to better understand these procedures.
1 - Solve the following equations:
See we have a split factor in fractions always seek the same elements in order to cancel. Note that n! It can be developed by the factor (n-2)! making have equal numbers in the numerator and denominator.
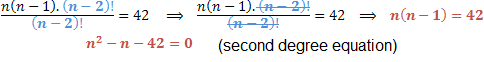
The factor has been eliminated from our equation leaving only the unknown. Therefore, we obtain an equation of the second degree in n unknown. Solving this equation we will obtain the following solutions.
Remember that the factor is only defined for natural numbers, that is, only for positive integers, so the solution n = - 6 is invalid for our factorial equation.
Again we must find a way to manipulate the factorial numbers so we can simplify them in this equation. Always seek to dismember the biggest factor number of expression in our example is the (n + 1)!
(n + 1)! = (n + 1). n!
Substituting into the equation, we have:
Now, there's only simplify the factorial (n-1)! and n !. Again we develop the biggest factor number, which is the n!
n! = n.(n - 1)!
Substituting into the equation:
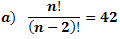
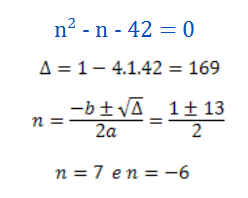
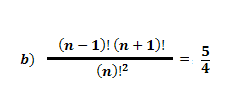

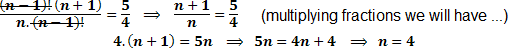
2 - Solve the equation:
There is the possibility to simplify these factor, however, note that we can build an equation of the second degree in which the unknown is n !. To better visualize, do the following replacement: n call by another letter, for example x.
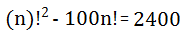
That is, x = n!
We obtain a new equation:

The x is related to the results of n! (Remember n! = X) so the second solution does not satisfy our equation. We now relate the first solution with the factorial.
n! = 120 (which number multiplied by its predecessors is equal to 120?)
n = 5
3 - Being n ≠ 0, select the alternative that has the values that satisfy the equation below:
a. 7
b. 0 and 7
c. 0 and 10
d. 1
e. 0 and 2
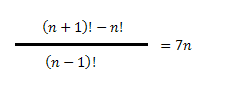
Note that the numerator we have two terms, carrying, share a split in two to facilitate the simplification of Factorial.
We get in the numerator factorial number that simplifies to (n-1) !
Therefore:
We determine two values for the unknown factor, however the initial condition of the problem is: n ≠ 0. Therefore, the only solution is that we can use n = 7.
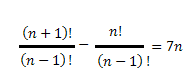

For today is all
math channel?
You gain a follower :)