Hi everyone, here's another post on "Math Problem and its Solution" for grade 9.
In this post I am going to present two ways of finding the solution to the following problem - there are lots of ways though. So here it goes!
Problem:

In this problem, let me illustrates angles of depression with reference to angles of elevation. But in order to solve the problem one should have a previous knowledge on special right triangle, both the 30˚- 60˚- 90˚ triangles theorem and the 45˚- 45˚- 90˚ triangles theorem. So with the special features of trigonometric ratios.
Recalling the following key terms
An angle of depression is the angle formed between the horizontal line and your line of sight when looking down.
In illustration:
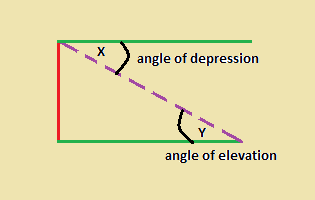
Now, supposed the spot on the object could look back up at you, another angle is formed, and this angle is called an angle of elevation. Based from the diagram, angle x and y form an alternate interior angles therefore, the angle of depression = angle of elevation.
Note:
The angle of depression is congruent to the angle of elevation, this assumes the object is close enough to the observer so that the horizontals for the observer and the object are effectively parallel. But this would not be the case for those objects that are already very far - like objects from outer space.
Back to the problem

Using two ways in solving the problem
- Special Right Triangle Theorems
- Trigonometric Ratios of Special Angles
Presentation of solution

Solution 1: Using Special Right Triangle Theorems
Illustration:
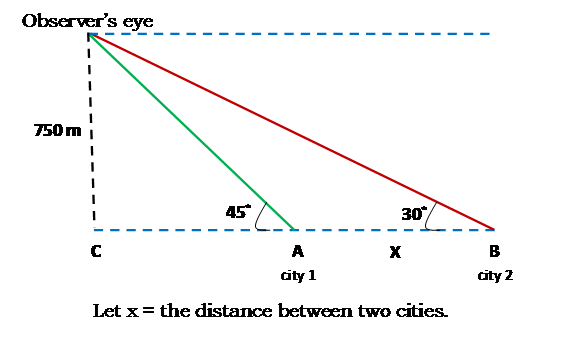


Solution 2: Using Trigonometric Ratios of Special Angles
Using the same figure above:



Both solutions obtained the value 549 m as the distance between two cities. It is therefore up to you which solution you are comfortable to use with. Any way it will give you both the correct answer.

Problem solved!
references:
- Math digest Geometry ( third quarter)
- http://www.mathwarehouse.com/geometry/triangles/right-triangles/special-right-triangles.php
- http://www.mathwords.com/a/angle_depression.htm
You got a 1.57% upvote from @postpromoter courtesy of @fabio2614!
Want to promote your posts too? Check out the Steem Bot Tracker website for more info. If you would like to support the development of @postpromoter and the bot tracker please vote for @yabapmatt for witness!
This post has received a 18.57 % upvote from @boomerang thanks to: @fabio2614
Great post. Is really nice description and solution.
thank you civilstudy for visiting my post