Combinatorics
”the branch of mathematics dealing with combinations of objects belonging to a finite set in accordance with certain constraints, such as those of graph theory.” – Google Definition

I loved this class. It makes things in probability so much easier! Here are a few great examples!
One
How many possible scantrons can a teacher receive if he has a test with 10 true/false questions?
Think of it this way… You have ten spots
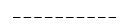
Each spot can have 2 possible answers, so we have
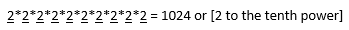
So, for fun, what is the probability that a student can guess all of the right answers? Well,
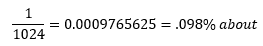
Not a chance. This is the reason why I am comfortable using T/F as a teacher. Haha.
Two
If there are 15 people in a race where the top 3 spots move on to the next race. How many possible orders can there be for the racers?
There are two ways to think about this…
A) Combinatorics: Use the same placement system we used in the last problem… 15 people can be first, 14 people can be second, and 13 people can be third. So,
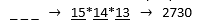
B) Probability: Since order matters and we are choosing 3 we can use a permutation [Remember that a combination is unordered]. The math looks like this:


Please keep these going! I used to love this stuff in school and enjoyed revisiting.
Absolutely will! Thanks for commenting!
It's been more than a decade when I last studied permutation and probability in school maths. Decades later, it feels good to see something that much mindtwisting. Haha!
Lol. Glad I could remind you of the horrors of math. Haha. It's one of my favorite lessons because it is easy to think about.
I'm not trained in math but I have gotten introduced to combinatorics in the last few months in the context of the study of GTO poker.
This post makes a friendly connection between the formula and real life application.
Oh yea. I need to do some studying for poker GT as well. I just went to the dog track the other day... Had 2 clubs in hand, Jack 10. 3 clubs on the flop. Another club on the turn. Other guy had the ace. I may have been able to bet him out early, but I doubt it.
Nice refresh of possibility and probability math for the summer. Thank you for the post.
No problem! Any time! See you again soon!
That would be great! Really interesting post and thanks for sharing!@hansenator,
Cheers and looking forward an another class~
Thank you! Many to come!
Here is a problem that will blow your mind if you haven't already done the calculation. Whats the probability of assembling my DNA at random? There are 3,000,000,000 base pairs in the human genome and 4 choices (codons) for each of the 3,000,000,000 base pairs. So the number of ways to assemble my DNA at random with replacement is 4^3,000,000,000. So the probability is 1/(4^3,000,000,000).
That is probably why no two people look exactly alike unless they are identical twins. The odds are literally astronomical.
It would take more than a quadrillion times the age of the universe just to assemble my DNA at random if you made one selection per day. Doing it twice? Thats not going to happen.
You are who you are. Lol.
That is a true statement.
Thank you!