The SHA256 algorithm can seem a little intimidating. I am going to do a few posts to break down the algorithm for you. My ultimate (unreachable) goal is to find the message (hex input) that corresponds to the hash of 0x0 (all zeroes) using a O(1) function (calculation - not brute force). I have my goal for 16 rounds solved with 2^(32*6) collisions, but have hit a wall with 17 rounds. I'm hoping you all can help. (These examples will be in next blogs)
So, presenting the SHA256 algorithm in living color!
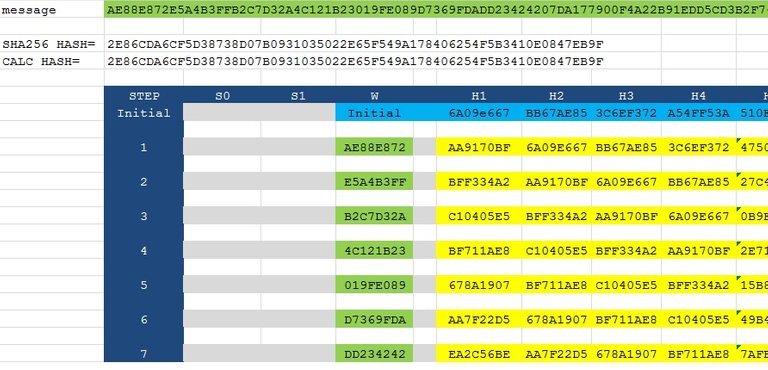
I have a MS Excel spreadsheet with all the formulas needed to calculate the rounds.
Green: Input Message (hexadecimal) AE88E872E5A4B3FFB2C7D32A4C121B23019FE089D7369FDADD23424207DA177900F4A22B91EDD5CD3B2F74D0A3606738A038AC89
Blue: Does not change. {For longer hashes, the initial hex is prior message digest. The "K" column on right never changes.}
Grey: Intermediate calculation
Yellow: Intermediate SHA256 Hash
high resolution image SHA256 rounds: http://extrazoom.com/image-64947.html?heuln50x50
**This is enough to understand the SHA256 algorithm. ** I will be dealing more with the calculation of the "A" column and "E" columns in the next blog to show that there is no hex string that maps to the 0x0 digest for less than 4
steps.
For the more detail oriented, below are the formulas.
Calculation of "W" column.
For i> 16, w(i) = w(i-16) + s0 + w(i-7) + s1
where
s0 = (w(i-15) rightrotate 7) xor (w(i-15) rightrotate 18) xor (w(i-15) rightshift 3)
s1 = (w(i-2) rightrotate 17) xor (w(i-2) rightrotate 19) xor (w(i-2) rightshift 10)
Calculation of Intermediate Hashes.
The new values are based on the values from the prior row. The intermediate calculations of
A=(H + W + K + ch + S1) + maj + S0
B=A of prior row
C=B of prior row
D=C of prior row
E= (H + W + K + ch + S1) + D
F=E of prior row
G=F of prior row
H=G of prior row
...Prior H value is thrown away....
where,
S1 = (E rightrotate 6)xor(E rightrotate 11)xor (E rightrotate 25)
ch = (E and F) xor ((not E) and G)
T1 = H + S1 + ch + K + W
S0 = (A rightrotate 2)xor (A rightrotate 13)xor (A rightrotate 22)
maj = (A and B) xor (A and C) xor (B and C)