In abstract terms: Given an N-element set, how many L-element subsets do we need so that every K-element subset is a superset of one of the L-element subsets? Let's express this by saying that the family of L-combinations "covers" the entire space of K-combinations.
In concrete terms: Suppose you're playing 17-card Chinese Poker, so your hand consists of K=17 cards from a standard N=52-card deck. We want to put your hand into a "bucket" labelled with L=5 cards, with all five cards appearing in your hand. (We're going to discard down to five cards that are the label of some bucket.) How many such buckets do we need, to have a bucket for any possible hand?
It's certainly possible for a hand to belong to more than one bucket (for a K-combination to be a superset of more than one L-combination), but we're interested in minimizing the number of buckets required, which should lead to fewer overlaps.
Small cases
For L=1 the solution is easy and provably minimal. The covering set needs to be of size N-K+1. Then every K-combination must overlap with at least one covering set, by the Pigeonhole principle. If the covering set is smaller, then we can choose K elements not in any of the 1-combinations.
Example: If N=5 and K=3 then our K-combinations are
For L=1 we need 3 L-combinations, which can just be 1, 2, 3. We can see that every 3-combination intersects one of the 1-combinations. But if we tried a smaller covering list like 1,2 then 345 is not covered.
What about L=2 or larger? This doesn't seem to be a trivial exercise.
For the N=5 K=3 case above, the set 12, 34, 35, 45 is a covering. We can prove this is minimal, because each 2-combination is a subset of at most three 3-combinations (we can only add one element, and there are three choices.) So three 2-combinations are not enough; that would only cover 9 elements.
A Lower Bound
This reasoning gives us a general lower bound:
Theorem: The minimum size of the (N,L)-combinations covering all (N,K)-combinations is at least
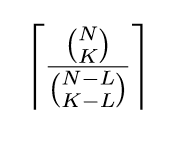
Proof: as above, each of the L-subsets can be expanded by choosing K-L of the remaining N-L elements of N. This gives the maximum size that an L-subset can cover, and so we need enough L-subsets to cover all (N choose K) possibilities.
Pigeonhole principle constructions
If we partition N into K-1 groups, then every K-combination contains at least two elements in one of the groups.
For example, with N=8 K=3, our groups can be 1234, 5678. Every 3-combination must pick at least two numbers from the front half, or the back half. So, we can cover those combinations with just 2 cards from every group: 12, 13, 14, 23. 24, 34, 56, 57, 58, 67, 68, 78. That is a covering set of size 12, and the formula above says the minimum is 8C3 / 6C1 = 10. Is there a better covering set, of size 10 or 11? (An exercise for the reader.)
This idea was suggested by Chris Hartman.
For a 17-card poker hand (N=52), this means we can find the following cover sets using this construction:
| L | groups | min in group | covering set size | lower bound |
|---|---|---|---|---|
| 2 | 16 groups, 4x4 and 12x3 | 2 | 4*(4C2) + 12*(3C2) = 60 | 10 |
| 3 | 8 groups, 4x6 and 4x7 | 3 | 4*(6C3) + 4*(7C3) = 220 | 33 |
| 4 | 5 groups, 3x10 and 2x11 | 4 | 3*(10C4) + 2*(11C4) = 1290 | 114 |
| 5 | 4 groups, 4x13 | 5 | 4*(13C5) = 5148 | 420 |
The last construction has an interpretation in terms of the suits: every 17-card hand must have at least five cards with the same suit.
Although this construction is straightforward and easy to automate, we are pretty far from the lower bound. Either we need a better lower bound, or a better construction.
Computer search?
For small examples we might be able to brute-force search all possible sets of L-combinations. But when N is even moderately sized, (N choose L) is large and the number of sets is exponentially greater. (52 choose 2) is 1326. To search for a 11-element covering set would require looking at (1325 choose 10) possibilities, about 10^24, unless we can considerably reduce the search space through symmetry arguments. Trying to find a 58- or 59- element covering set would be more like 10^102 possibilities.
So exhaustive search is right out (and thus minimality will probably be hard to prove) but we could do a greedy search. At each step, count the number of K-combinations not yet covered, and pick an L-combination that picks a maximal number of them. When (N choose K) is large, even this is challenging; is there any efficient way to judge whether a set of L-combinations covers all the K-combinations?
Here's some Python code that does a pretty crude greedy search:
import itertools
N = 10
K = 5
L = 3
kcombs = list( set(x) for x in itertools.combinations( range( 1, N+1 ), K ) )
lcombs = list( set(x) for x in itertools.combinations( range( 1, N+1 ), L ) )
cover = []
def removeCovered( lc ):
global kcombs
kcombs = [ x for x in kcombs if not lc.issubset( x ) ]
def countCovered( lc ):
return sum( 1 for x in kcombs if lc.issubset( x ) )
def greedySearch():
global lcombs
first = lcombs.pop()
removeCovered( first )
print first
cover.append( first )
while len( kcombs ) > 0:
nonzero = []
maxCoverage = 0
maxSet = None
for lc in lcombs:
c = countCovered( lc )
if c > maxCoverage:
maxCoverage = c
maxSet = lc
if c > 0:
nonzero.append( lc )
print maxSet, maxCoverage
cover.append( maxSet )
removeCovered( maxSet )
kcombs = nonzero
print len( cover ), "elements in cover"
for c in cover:
print ",".join( str(x) for x in c ), " ",
print
Run with the parameters provided it found a 22-element cover; the formula above gives a lower bound of 12. The best pigeonhole construction we could do would be to partition the numbers into two groups of five each, which gives us a 2*(5C3) = 20-element cover. So the greedy search algorithm didn't do as well as we know to be possible (which isn't too surprising.)
Randomizing the list of combinations to search actually does worse; mostly we get 23- and 24- elements covers, but once I saw 21.
Open problems
Is the pigenhole-based construction the best possible? If not, can we provide an example? If so, can we prove it and thus improve our lower bound?
Motivation
I invented a data structure several years ago which I was planning to write up in a future article, which uses these minimum covering sets to create indexes. Here's the links to my old blog in case I don't get around to it:
https://markgritter.livejournal.com/607171.html
https://markgritter.livejournal.com/607693.html
I am wondering if the same ideas can be applied to multisets to solve word games.
we love coding

Reply !stop to disable the comment. Thanks!Hello! Your post has been resteemed and upvoted by @ilovecoding because ! Keep up good work! Consider upvoting this comment to support the @ilovecoding and increase your future rewards! ^_^ Steem On!
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Hi @markgritter!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Exhaustive search on L=2 for small values shows that the construction above finds the optimal, but there is not much of a gap between the lower bound and the pigeonhole construction anyway.
The optimal covering found for the (9,4,2) case is 12 13 23 45 46 56 87 97 89 which is precisely the pigeonhole construction using partition (1,2,3) (4,5,6) (7,8,9).
The construction does fail to be optimal for cases like N=7 K=6 L=5 where there is a trivial cover of size 4. But since C(7,6) is isomorphic to C(7,1) this is not a very interesting case.