In this video I go over further into differential equations and expand on my earlier videos on modeling population growth. The same basic model used in modeling population growth occurs actually very often in nature: in bacteria growth, radioactive decay, and compound interest, to name only a few. This model stems from the idea that the rate of change, either growth or decay, of a substance is often proportional to the amount of that substance. In other words, doubling the amount of a substance often doubles the rate of change as well. The result is a simple separable differential equation and the solution is an exponential function. This is a very interesting and important video because of the many applications that used the resulting solution, so make sure to watch this video!
Watch on DTube:
Watch on BitChute: https://www.bitchute.com/video/XbHvhmNDdZ9B/
Watch on YouTube: https://youtu.be/DZtDUIZuxcg
Download PDF Notes: https://1drv.ms/b/s!As32ynv0LoaIhtATE4Zy5KKR3_5Htw
View Video Notes Below!
Download These Notes: Link is in Video Description.
View These Notes as an Article: https://steemit.com/@mes
Subscribe via Email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donateReuse of My Videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight Back Against Censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Join my private Discord Chat Room: https://mes.fm/chatroom
Check out my Reddit and Voat Math Forums:
Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Follow My #FreeEnergy Video Series: https://mes.fm/freeenergy-playlist
Watch my #AntiGravity Video Series: https://mes.fm/antigravity-playlist
Follow My #MESExperiments Video Series: https://mes.fm/experiments-playlist>
NOTE: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (If Available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed. (#Try2xSpeed)
-- Try 4X+ Speed by Browser Extensions, HookTube.com, Modifying Source Code.
-- Browser Extension Recommendation: https://mes.fm/videospeed-extension- Download and Read Notes.
- Read notes on Steemit #GetOnSteem
- Watch the video in parts.
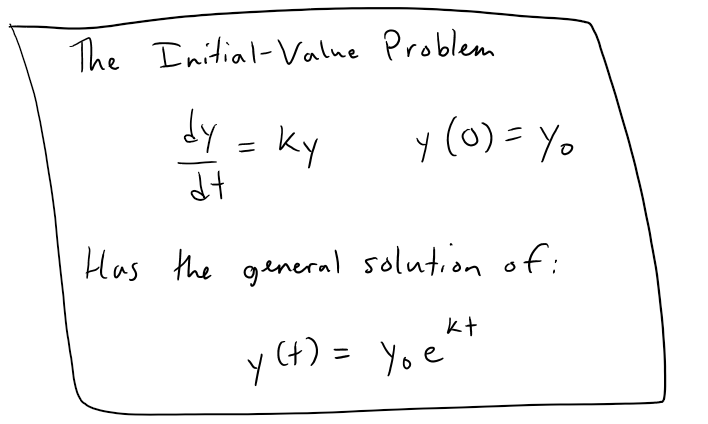
Differential Equations: Exponential Growth and Decay
One of the models for population growth, which I went over in my earlier videos, was based on the assumption that the population grows at a rate proportional to the size of the population:
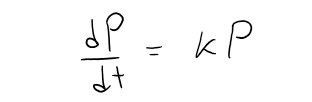
Is that a reasonable assumption?
Suppose we have a population (of bacteria, for instance) with size P = 1000 and at a certain time it is growing at a rate of P' = 300 bacteria per hour.
Now let's take another 1000 bacteria of the same type and put them with the first population.
Each half of the new population was growing at a rate of 300 bacteria per hour.
We would expect the total population of 2000 to increase at a rate of 600 bacteria per hour initially (provided there's enough room and nutrition).
So if we double the size, we double the growth rate.
In general, it seems reasonable that the growth rate should be proportional to the size.
The same assumption applies in other situations as well.
In nuclear physics, the mass of a radioactive substance decays at a rate proportional to the mass.
In chemistry, the rate of a unimolecular first-order reaction is proportional to the concentration of the substance.
In finance, the value of a savings account with continuously compounded interest increases at a rate proportional to that value.
In general, if y(t) is the value of a quantity y at time t and if the rate of change of y with respect to t is proportional to its size y(t) at any time, then:
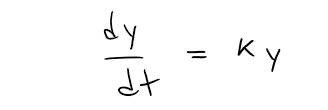
Where: k is a constant.
This equation is sometimes called the:
- Law of natural growth (if k > 0)
- Law of natural decay (if k < 0)
Because it is a separable equation we can solve it by the methods shown in my earlier videos:
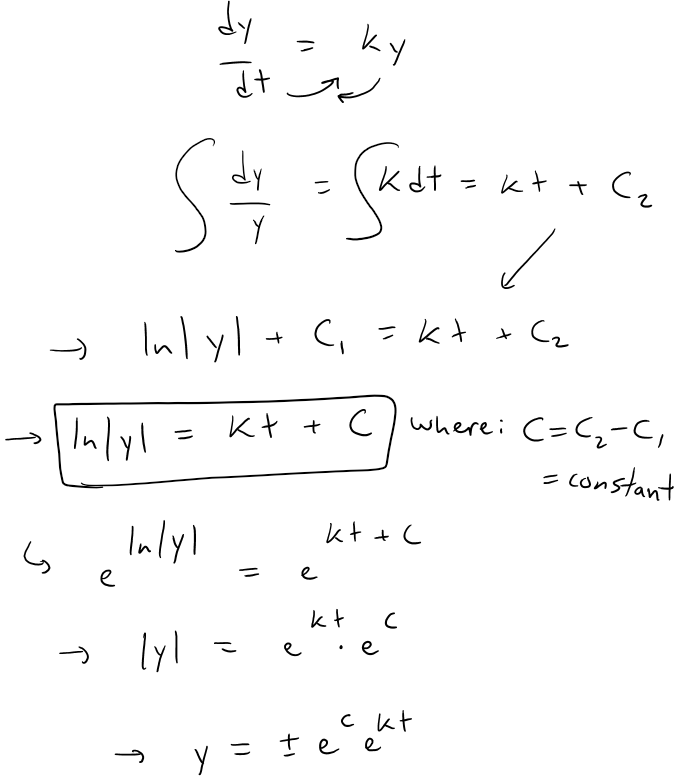
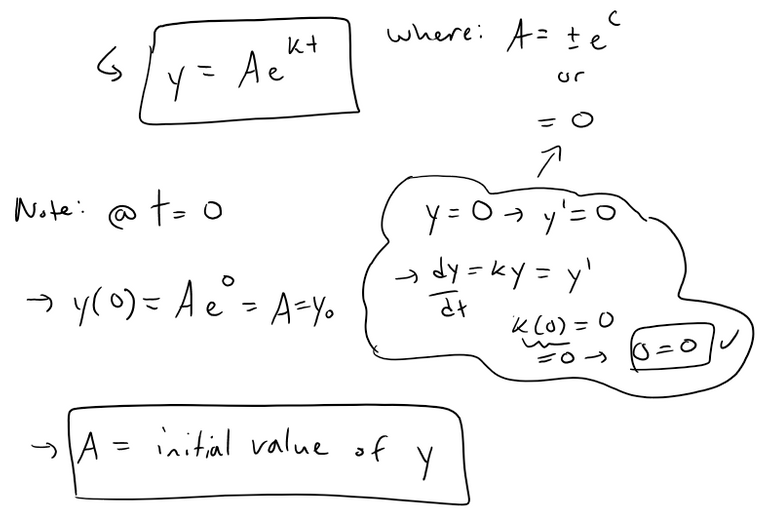
Because this equation occurs so frequently in nature, we summarize what we have just proved for future use: