In this video I go over part 2 of the example which I covered in my last video on modifying the Lotka-Volterra equations for predator-prey systems by using a logistic model growth rate for the prey population. In that part I went over the equilibrium solutions, and in this part I take a look at a phase trajectory of the predator-prey, or wolf-rabbit, populations. I also sketch the possible graph of the populations of each species through time, which shows how the populations fluctuate until they stabilize at a specific level. This is a very interesting video on modeling populations of predator-prey type animals so make sure to watch this video!
Watch on DTube:
Watch on BitChute: https://www.bitchute.com/video/emaKXFJYovGV/ Download PDF Notes: https://1drv.ms/b/s!As32ynv0LoaIht148ZIXopQ597LynQ
View Video Notes Below!
Download These Notes: Link is in Video Description.
View These Notes as an Article: https://steemit.com/@mes Subscribe via Email: http://mes.fm/subscribe Donate! :) https://mes.fm/donateReuse of My Videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight Back Against Censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Join my private Discord Chat Room: https://mes.fm/chatroom
Check out my Reddit and Voat Math Forums:
Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook Watch my #AntiGravity Video Series: https://mes.fm/antigravity-playlist Follow My #FreeEnergy Video Series: https://mes.fm/freeenergy-playlist
NOTE: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions
- Play this video at a faster speed.
--TOP SECRET LIFE HACK: Your brain gets used to faster speed. (#Try2xSpeed)
--Try 4X+ Speed by Browser Extensions, HookTube.com, Modifying Source Code.
--Browser Extension Recommendation: https://mes.fm/videospeed-extension- Download and Read Notes.
- Read notes on Steemit #GetOnSteem
- Watch the video in parts.
Example:
In Example 1 (https://youtu.be/dkQYqI4FXxA), we used Lotka-Volterra equations to model populations of rabbits and wolves.
Let's modify those equations as follows:
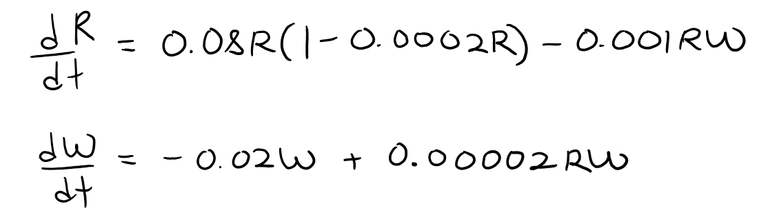
a) According to these equations, what happens to the rabbit population in the absence of wolves?
b) Find all the equilibrium solutions and explain their significance.
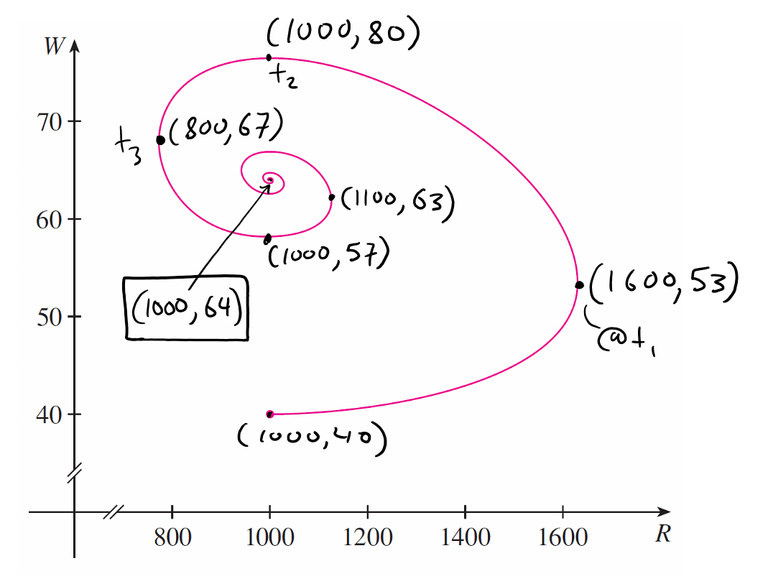
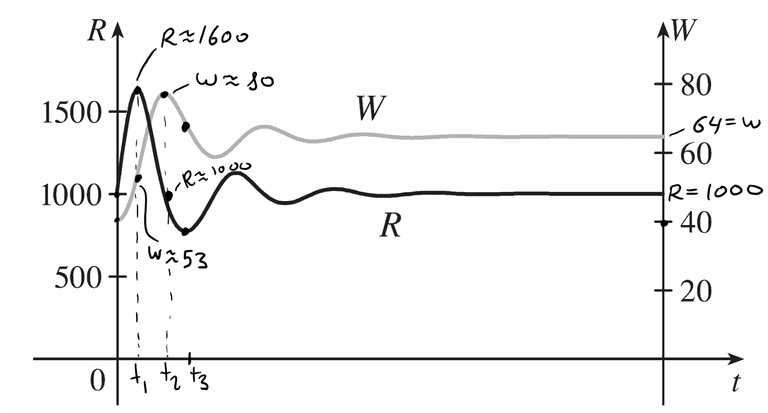
c) The figure shows the phase trajectory that starts at the point (1000, 40).
Describe what eventually happens to the rabbit and wolf populations.
Reveal spoiler
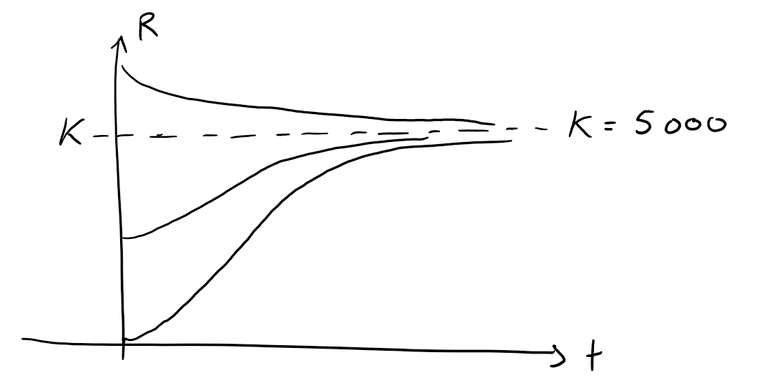
d) Sketch the populations of the rabbit and wolf populations as functions of time.
Solution:

Recall the Logistic Equation (https://youtu.be/FMFTLa8URDg):
Thus in the absence of wolves, the rabbit population stabilizes at 5000.
b) R and W are constant when R' = 0 and W' = 0:
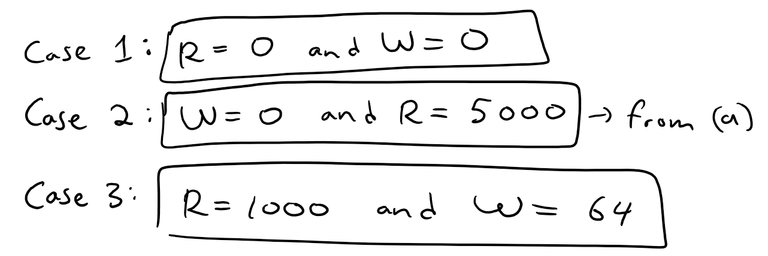
Significance of each case:
Case 1: Both populations are zero so can't grow.
Case 2: With no wolves present, the rabbit population maxes out at 5000.
Case 3: The predator/prey interaction balances out and the populations are stable.
c) The populations of wolves and rabbits fluctuate around 64 and 1000, respectively, and eventually stabilize at those values.
d) A sketch of the rabbit and wolf populations with time is shown below:
Hmmmmm.... Can you compute for humans my friend? I meant the ones who fleece others (the bankers as predator) as opposed to the ones who were gutted out (the ordinary people)?
Hihi.... Very interesting concept to MATH as I do not even know these things are "computable".
Ahhh yes, these concepts are essentially what the rulers of this world use to maintain global control. That is there is lots of "population-control" propaganda. Best to fight outside the system!