Review With Me #3 | Algebra | Five Equalities of Real Numbers Explained

Algebra is defined from Google as the part of mathematics in which letters and other general symbols are used to represent numbers and quantities in formulae and equations. Personally, I believe that Algebra is the foundation and the root of all the branches of Mathematics. In this session, we will be tackling the "Equality of Real Numbers."

Numbers vs Real Numbers

Sounds the same, right? Some people may confuse, but there is a big difference between the two. A number is an arithmetical value, expressed by a word, symbol, or figure, representing a particular quantity and used in counting and making calculations and for showing order in a series or for identification. There are a lot of kinds of a number.

In contrast, Real Numbers are our "known" numbers. Simply, Real Numbers are the numbers along with the Cartesian Plane ( includes ALL rational numbers, integers, irrational numbers and fractions.)

What is Equality?

As we know literally, an equality means equal; the same. In government and politics, it talks about status, rights and opportunities. But in Mathematics, it symbolizes and shows relationship between the two quantities or expressions having a symbol of " = " (read as equals).

Equality of Real Numbers

For all real numbers a, b, and c, the following are the properties.

Reflexive Property: a = a.
It is simply defined as an any value that is equal to itself. For example:

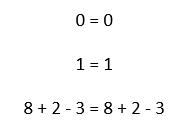
Obviously, 0 = 0 is a reflexive property for zero is just equal to itself. Same as on the equation/expression, the arrangement and answer on the left side is just a "reflex" to the second one.
Symmetric Property: If a = b, then b = a.
This simply explains that if one value is equal to another value, then the second value is also equal to the first value. For example:

Here's my technique, I can say when it is a Symmetric Property when it is just a reverse in given equation from the first one. Our first statement says that 3 + 4 is equal to 7; therefore, 7 is equal to the sum of 3 and 4.
Transitive Property: If a = b and b = c, then a = c.
This talks about that if the first value is equal to the second value, and the second value is equal to the third value, then the first value is equal to the third value. Like for example:
Addition Property: If a = b, then a + c = b + c and c + a = c + b.
This shows that the same value must be added to the first and second expressions. For example:

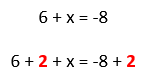
The main idea here is to keep it balance by adding the same values in both side.
Multiplicative Property: If a = b, then ac = bc and ca = cb.
The same as the idea of Addition Property, the same value must be multiplied to the first and second expressions to keep both in balance. For example:

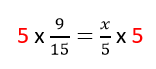
Another set of examples:

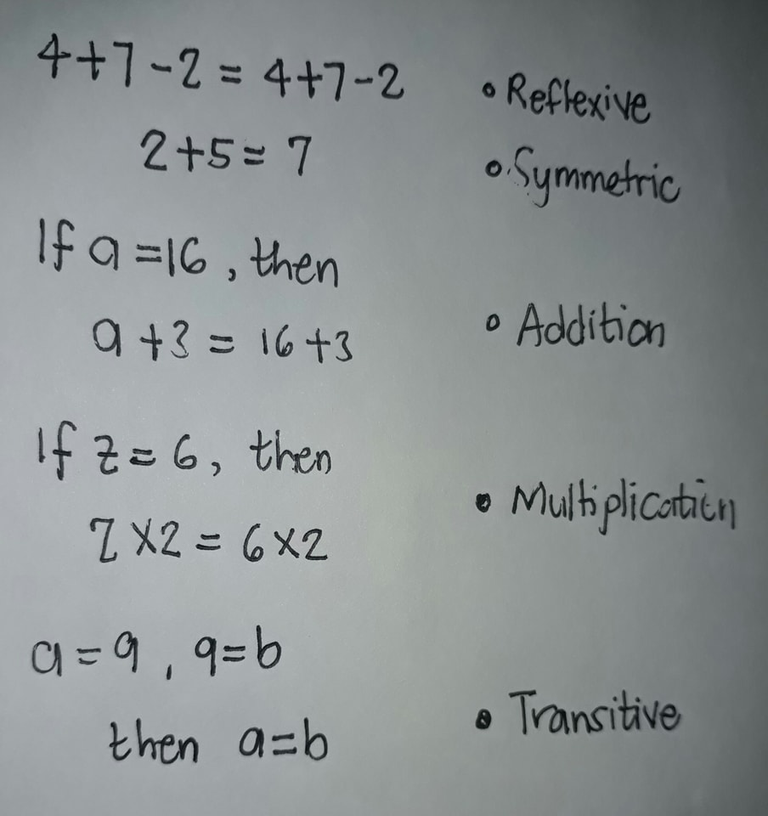
Basically, each property is very simple if we have to understand its principle clearly.

Thank you folks! I am excited to share more with you about the learning I got on engineering.

@mikekenlytungal

[ Image Source ]
[ Reference A ]
[ Reference B ]

The content is mine.