Elements of Set Theory: Algebra of Sets
The two basic operation on sets are
operation of union
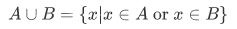
operation of intersection
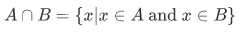
We also have the operation relative complement 
of B in A:
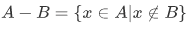
(some books denotes relative complement as A\B)
The usual diagram is shown below:
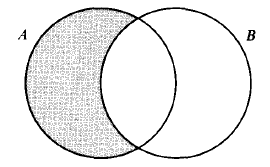
Note that the union axiom was used to give us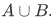 
. But the intersection operation 
and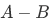 
were both obtained from subset axioms.
Interestingly, there is no such thing as the "absolute complement" of, let say B, such that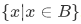
. This is not a set for once you use union operation with B it would be the class of all sets. In any way, it is unlikely to be an interesting object of study.
Let's say we are studying sets of real numbers. Let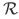 
be the set of all real numbers, and suppose that 
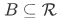. Then the relative complement of 
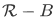consists of these real numbers, not in B. On the other hand, the absolute complement of B would be a huge class containing all manner of irrelevant things; it would contain any set that was not a real number.
Let's consider the following set.
- let A be the set of all left-handed people
- let B be the set of all blond people
- let C be the set of all male people
Consider the following cases:
1.
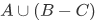is the set of all people who are either left-handed or are blond females (or both).
- is the set of all females who are either left-handed or blond (or both).
Assume we have a friend named Joe (who is a left-handed male). Looking from the two cases above, he belong to the first case but not the second.
Algebra of Sets
The study of the operations of union 
, intersection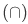 
, and relative complementation 
, together with the inclusion relation 
goes by the name of algebra of sets. This operations are analogous to the ones in real numbers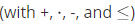 
, but there are significant differences.
Here are the identities, which hold for any sets, which are elementary facts of the algebra of sets,
Commutative laws
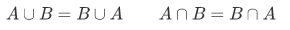
Associative laws
Distributive laws
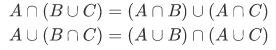
De Morgan's laws
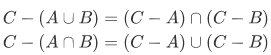
Identities involving emptyset
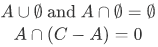
Most of the time when we consider sets, we are dealing with sets which are subsets of some large set or "space" S. Example of this study of subsets deals with space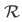 
of real numbers.
For this cases of subsets, let say A and B of space S, we can abbreviate it as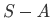 
as simply 
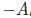, the space set S being understood as fixed. In this form, De Morgan's laws become
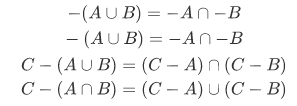
Elements of Set Theory: Epilogue
We've introduced six of the ten axioms of this book.
- 5 axioms
- 1 axiom schema (an axiom schema is an infinite bundle of axioms, such as the subset axioms.)
Disclaimer: this is a summary of section 2.3 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshot from generated latex form using typora
Thank you for reading ...
This post has received a 8.33% upvote from @msp-bidbot thanks to: @sinbad989. Delegate SP to this public bot and get paid daily: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP Don't delegate so much that you have less than 50SP left on your account.