Previously, we have the union axiom in its preliminary form, this union operation allowed us to form the union of two sets. And by repeating the process, we can form the union of three sets or the union of forty sets.
How do we go with infinite sets?
Suppose we have an infinite collection of sets
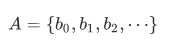
We want the union of all the sets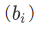 
in A. For this we need a more general union operation:
So we have a new definition for union, such that for any set A, the union of 
of A is the set defined by
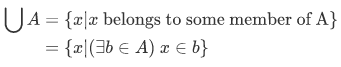
We can see that the general union form 
is like a melting pot into which all members of A are dumped. This concept is understood if supported by some example. Consider the set of countries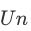 
belong to the United Nations. Then 
is the set of all people that are citizens of some country belonging to the United Nations.
For smaller set example, consider the following:
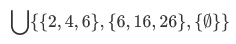
If we evaluate this using the definition of the general union operation, we have:
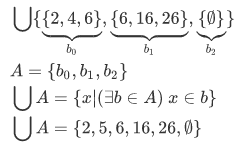
Our new set is now consists of six numbers.
And now, we can improved our preliminary definition of the union axiom to know that a set exists containing the members of the members of A.
Union Axiom For any set A, there exists a set B whose elements are exactly the members of the members of A:
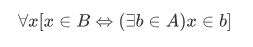
We can state the definition of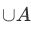 
in the following form:
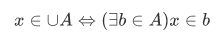
For example,
With this form, our preliminary definition of union in section 2.1 can be discarded in favor of the new form.
Similarly we have
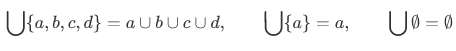
Similarly, we should also introduce a corresponding generalization of the intersection operation. Suppose we want to take the intersection of infinitely many sets 
. Then we have
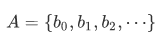
the desired intersection can be informally characterized as
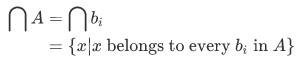
In general, we define for every nonempty set A, the intersection of A by the condition,
The thing about intersection operation is that, unlike union operation, intersection operation does not require special axiom but a theorem. We introduce the following theorem.
Theorem 2B For any nonempty set A, there exists a unique set B such that for any x,
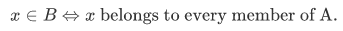
Proof:
We are given that A is nonempty; let c be some fixed member of A. Then by a subset axiom there is a set B such that for any x,
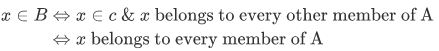
Uniqueness follows from extensionality.
Examples:
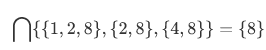
Note that when A becomes larger, 
gets smaller. For instance,
Also, whenever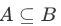 
then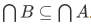 
. There is one troublesome extreme case.
What happens if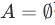 
?
Now for this case, any x at all belongs to every member of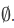 
. (There can be no member of 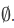to which x fails to belong.) Thus it looks as if $\cap 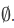$ should be the class V of all sets.
Using theorem 2A, we can show that there is no set C such that for all x,
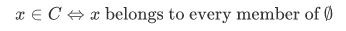
since the right side is true for every x.
This is actually notational problem: how do we define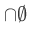 
? This situation is analogous to division by zero in arithmetic. How does one define 
?
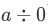The simplest option is to leave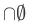 
undefined, since there is no very satisfactory way of defining it. For some logicians, this is not good as it leaves an untidy loose end and in later times they may trip over this problem.
The other option is to select some arbitrary scapegoat and define
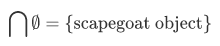
The thing is, whenever one forms the infinite intersection of 
one should be aware of the possibility that we may have an empty set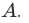 
.
Example:
If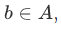 
, then 
This follows from the definition of union Since $b$ is an element of A, it is an element of the new set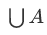 
which contains all element of the element of A.
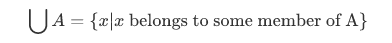
Example
If 
, then 
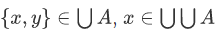and 
.
The element of a union of $A$ is also an element of the union of the the union of $A$. Other way of expressing this is as follows.
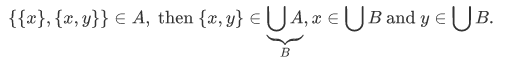
Example
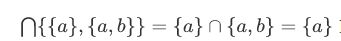Hence
Disclaimer: this is a summary of section 2.2 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshot from generated latex form using typora
You got a 26.32% upvote from @moneymatchgaming courtesy of @sinbad989! Please consider upvoting this post to help support the MMG Competitive Gaming Community.